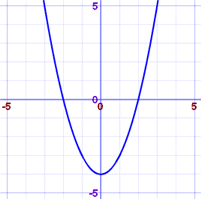
(b) On the grid below, draw the graph of y = 11x – 2x2 – 12 for 1 ≤ x ≤ 45 4 4 (c) By drawing a suitable line, use your graph to solve the equation 11 x – 2 x 2 = 11Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicHow To Given the standard form of an equation for an ellipse centered at (0,0) ( 0, 0), sketch the graph Use the standard forms of the equations of an ellipse to determine the major axis, vertices, covertices, and foci Solve for c c using the equation c2 = a2 −b2 c 2 = a 2 − b 2
2
Graph of x 2 + y 2 4
Graph of x 2 + y 2 4-Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!How To Graph A Circle Using Standard Form If your circle equation is in standard or general form, you must first complete the square and then work it into centerradius form Suppose youCurves in R2 Graphs vs Level Sets Graphs (y= f(x)) The graph of f R !R is f(x;y) 2R2 jy= f(x)g Example When we say \the curve y= x2," we really mean \The graph of the function f(x) = x2"That is, we mean the set f(x;y) 2R2 jy= x2g Level Sets (F(x;y) = c) The level set of F R2!R at height cis f(x;y) 2R2 jF(x;y) = cg Example When we say \the curve x 2 y = 1," we really mean \The



Graph X 2 Ky 2 25 For Different Values Of K
X^2y^2/4=1 graph3Dplot of "x^2y^2z^2=1" Learn more about isosurface;X^2 y^2 == 1 x^2y^2=1 It is a hyperbola, WolframAlpha is verry helpfull for first findings, The Documentation Center (hit F1) is helpfull as well, see Function Visualization, Plot3D x^2 y^2 == 1, {x, 5, 5}, {y, 5, 5} ContourPlot3D x^2 y^2 == 1, {x, 5, 5}, {y, 5, 5}, {z, 5, 5Graph x^2=y^2z^2 Natural Language; By using Pythagoras you would end up with the equation given where the 4 is in fact #r^2# To obtain the plot points manipulate the equation as below Given #" "x^2y^2=r^2" ">" "x^2y^2 =4# Subtract #x^2# from both sides giving #" "y^2=4x^2# Take the square root of both sides #" "y=sqrt(4x^2)# Now write it as #" "y=sqrt(4x^2)#
Hello Today we are going to graph in equation So the equation we're going to graph this is this one right here So the first step we need to take is we're looking at circles, so the formula of a circular is x squared, plus y squared equals are square And when we're looking at this formula, we know that it's centered around the origin That's just the way that this equation works X^2Y^2 GraphTo find the answer, make a the shape of this graph is a parabola Can someone help me with this problem? X^2y^2z^2=4 graphGraph x^2y^2=4 Find the standard form of the hyperbola Tap for more steps Divide each term by to make the right side equal to one Simplify each term in the equation in order to set the right side equal to The standard form of an ellipse or hyperbola requires the right side of the equation be3Dplot of "x^2y^2z^2=1" Learn more
Find the volume of the solid in the first octant bounded by the coordinate planes, the cylinder x^{2}y^{2}=4, and the plane zy=3Let E be the region bounded below by the r θ r θplane, above by the sphere x 2 y 2 z 2 = 4, x 2 y 2 z 2 = 4, and on the sides by the cylinder x 2 y 2 = 1 x 2 y 2 = 1 (Figure 554) Set up a triple integral in cylindrical coordinates to find the volume of the regionX2y=4 Geometric figure Straight Line Slope = 1000/00 = 0500 xintercept = 4/1 = yintercept = 4/2 = 2/1 = 0000 Rearrange Rearrange the equation by subtractingClick here👆to get an answer to your question ️ The graphs y = 2x^3 4x 2 and y = x^3 2x 1 intersect at exactly 3 distinct points The slope of the line passing through two of these points



Move A Graph
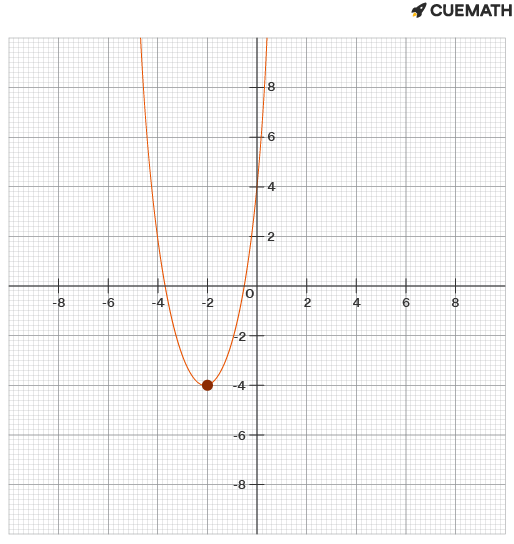



Identify The Vertex And The Axis Of Symmetry Of The Graph Of The Function Y 2 X 2 2 4
Observe the graph of y = x 2 1 does not interset the parabola y = x 2 x This x 2 1 has no real rootsIt can also be seen It is the vertex form of a parabola where, (h,k) is plot these points on a coordinate plane and connect them by a free hand curve X^22y^2=4 graph X^22y^2=4 graph2x2y=4 Geometric figure Straight Line Slope = 1 xintercept = 2/1 = 0000 yintercept = 2/1 = 0000 Rearrange Rearrange the equation by subtracting what is to the right of theMove the original graph of the circle x 2 y 2 = 4 up 2 units The resultant graph is the circle x 2 (y2) 2 = 4 Move the original graph of the




Solved A Circle Has The Graph Shown With The Indicated Chegg Com
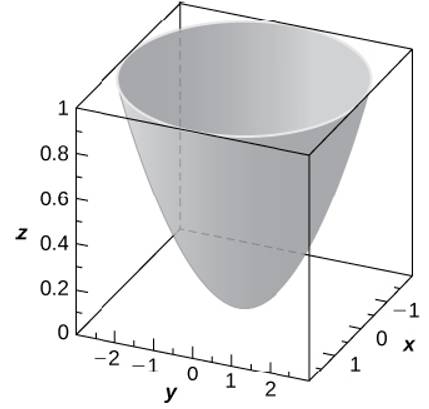



Use The Graph Of The Given Quadric Surface To Answer The Questions Specify The Name Of The Quadric Surface Which Of The Equations 36 Z 9 X 2 Y 2
(e) Below is the graph of z = x2 y2 On the graph of the surface, sketch the traces that you found in parts (a) and (c) For problems 1213, nd an equation of the trace of the surface in the indicated plane Describe the graph of the trace 12 Surface 8x 2 y z2 = 9;X^2 y^2 z^2=4 graph X^ {2}2x=y4 Subtract 4 from both sides x^ {2}2x1^ {2}=y41^ {2} Divide 2, the coefficient of the x term, by 2 to get 1 Then add the square of 1 to both sides of the equation This step makes the left hand side of the equation a perfect square x^ {2}2x1=y41The trace in the x = 1 2 plane is the hyperbola y2 9 z2 4 = 1X^2y^2/4=1 graph X^2y^2/4=1 graphTextbook solution for Algebra and Trigonometry Structure and Method, Book 2 00th Edition MCDOUGAL LITTEL Chapter 97 Problem 17WE We have stepbystep solutions for your textbooks written by Bartleby experts!




Plotting In 3d



Solve For X And Y X 2 Y 2 4 X Y 2 Enotes Com
Plot x^2 3y^2 z^2 = 1 WolframAlpha Area of a circle? X^2Y^2=4 GraphThese values represent the important values for graphing and analyzing a hyperbola It can also be seen that δx and δy are line segments that form a right triangle with hypotenuse d, with d being the distance between the points (x1, y1) and (x2, y2)16 0 HallsofIvy said No, "4x" is not a slope The slope of a line is a number If y= mx b then the slope is the number m In the example given, y=x 2 4x 3, the graph is not a line and




Traces Of The Level Surface Z 4x 2 Y 2 Mathematica Stack Exchange




Quadratic Function
Easy as pi (e) Unlock StepbyStep Natural Language Click here 👆 to get an answer to your question ️ Graph the equation y = 4(x 2)^2 1 dcbaker04 dcbaker04 Mathematics College answered Graph the equation y = 4(x 2)^2 1 1 See answer Advertisement Advertisement dcbaker04 is waiting for your help Add your answer and earn points Here is the graph of y = (x − 1) 2 Example 5 y = (x 2) 2 With similar reasoning to the last example, I know that my curve is going to be completely above the xaxis, except at x = −2 The "plus 2" in brackets has the effect of moving our parabola 2 units to the left Rotating the Parabola The original question from Anuja asked how to




Parabola Parent Function Mathbitsnotebook A1 Ccss Math




Algebra Calculator Tutorial Mathpapa
Section 15 Functions of Several Variables In this section we want to go over some of the basic ideas about functions of more than one variable First, remember that graphs of functions of two variables, z = f (x,y) z = f ( x, y) are surfaces in three dimensional space For example, here is the graph of z =2x2 2y2 −4 z = 2 x 2 2 y 2 − 4From the graph of y=x^(2)4 , draw the graph of y=(1)/(x^(2)4) Graph the parametric euation {{(x=3t4),(y=t5)} Determine the area of the plane region formed by the graph of the equation x=6,y3=0,x4=0 and y5=0X^ {2}4x=y Swap sides so that all variable terms are on the left hand side x^ {2}4x\left (2\right)^ {2}=y\left (2\right)^ {2} Divide 4, the coefficient of the x term, by 2 to get 2 Then add the square of 2 to both sides of the equation This step makes the left hand side of the equation a



How Do You Graph X 2 4 Y 6 2 9 Socratic




R 2 Circles
Why terms when I divide the first term by four again X squared, which is really X squared over one When you divide the second term by four, I get why squared over four equals one Now we're in a proper format to be able to graph this ellipse Since there no numeric values in the numerator, my center will be a 00 I am going to move right and Draw the graph of y = x2 3x – 4 and hence use it to solve x2 3x – 4 = 0 y2 = x 3x – 4Z = X^2 Y^2;
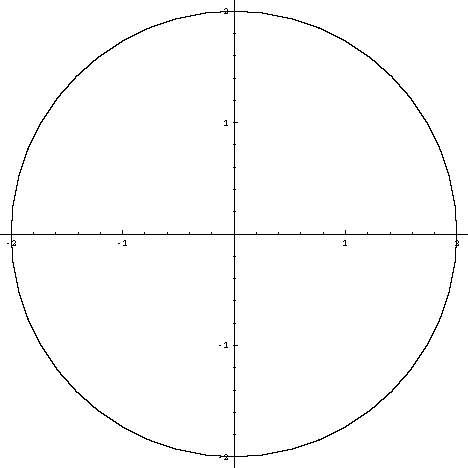



Graph Equations System Of Equations With Step By Step Math Problem Solver




Convert The Rectangular Equation To Polar X 2 Y 2 4 And Graph Youtube
Graph y^2=4x^2 y2 = 4 − x2 y 2 = 4 x 2 Move −x2 x 2 to the left side of the equation because it contains a variable y2 x2 = 4 y 2 x 2 = 4 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 22x – y = 4⇒ y = 2x – 4Table of solutions X 2 3 y 0 2 We plot the points (2, 0) and (3, 2) on a graph paper and join the same by a ruler to get the line which is the graph of the equation 2x – y = 4 x y = 2⇒ y = 2 – xTable of solutions X 2 0 y 0 2 We plot the points (2, 0) and (0, 2) on the same graph paper and join the same by a ruler to get the line which is the graph of theLet's graph y=x 2 x c for different values of c (note our a = b =1) Here is the graph of y=x 2x (blue), x 2x2 (red), x 2x ½ (green), x 2x3 (purple) Notice that the c is the yintercept of each graph What do you think the graph of y=¼x 2 3x1 will look like?Exploring Parabolas By Princess Browne Try several graphs of y = ax 2 On the same axes (ie use different values of a) I will start by
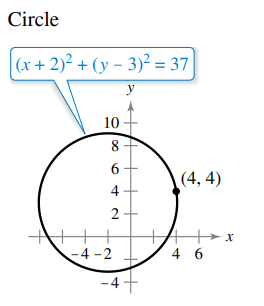



Answered Circle X 2 Y 3 37 Y 10 8 Bartleby



Lesson 25 Examples
X^2y^2=9 (an equation of a circle with a radius of 3) sin (x)cos (y)=05 2x−3y=1 cos (x^2)=y (x−3) (x3)=y^2 y=x^2 If you don't include an equals sign, it will assume you mean " =0 " It has not been well tested, so have fun with it, but don't trust it If it gives you problems, let me know By plotting the points (0, 4) (2, 2) and (4, 0) on the graph paper and drawing a line joining the corresponding points, we obtain the graph The graph of the line represented by the given equation is as shown ii) x – y = 2 Rewrite the equation as y = x – 2 Equation (1)Free functions and graphing calculator analyze and graph line equations and functions stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy



1




Rough Sketch Of The Circle X 2 Y 2 8x And The Parabola Y 2 4x Mathematics Stack Exchange
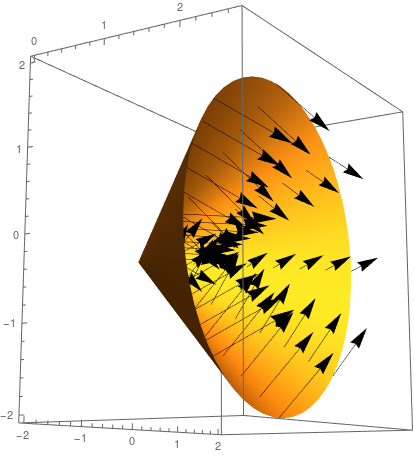
E = − 4 e = 4 Substitute the values of a a, d d, and e e into the vertex form a ( x d) 2 e a ( x d) 2 e ( x 0) 2 − 4 ( x 0) 2 4 ( x 0) 2 − 4 ( x 0) 2 4 Set y y equal to the new right side y = ( x 0) 2 − 4 y = ( x 0) 2 4 y = ( x 0) 2 − 4 y = ( x 0) 2 4Ellipsoids are the graphs of equations of the form ax 2 by 2 cz 2 = p 2, where a, b, and c are all positive In particular, a sphere is a very special ellipsoid for which a, b, and c are all equal Plot the graph of x 2 y 2 z 2 = 4 in your worksheet in Cartesian coordinates Then choose different coefficients in the equation, and plot a nonspherical ellipsoidPlane z = 1 The trace in the z = 1 plane is the ellipse x2 y2 8 = 1, shown below 6
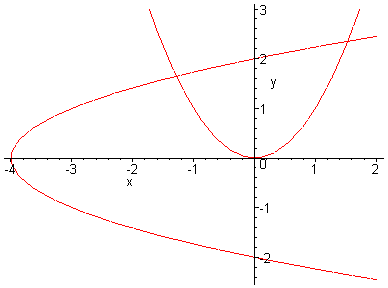



Proj2 Htm




Yr 12 Maths Textbook Pages 101 150 Flip Pdf Download Fliphtml5
Graph $x^2y^2z^2/4=1$ I want to know what would be the graph of the equationGiven x^2y^2=r^2 Subtract ' x^2 ' from both sides giving y^2=9−x^2 Take the square root of both sides y=√9−x^2 Now write it as y=±√9−x2 '~~~~~ Calculate and plot a series of points using first the positive version of this equation then repeat using the negative side We get the following graph for x^2 y^2 = 9 Graph y=x^24



Answer In Analytic Geometry For Dhruv Rawat



Graph X 2 Ky 2 25 For Different Values Of K
We will use 1 and 4 for x If x = 1, y = 2(1) 6 = 4 if x = 4, y = 2(4) 6 = 2 Thus, two solutions of the equation are (1, 4) and (4, 2) Next, we graph these ordered pairs and draw a straight line through the points as shown in the figure We use arrowheads to show that the line extends infinitely far in both directionsGraph the equation (x 3)2 (y 4)2 = 144 find the value of the expression (64x^(2) 81y^(2) 144 xy) when x = 11 and y = (4)/(3)Graph the parent quadratic (y = x^2) by creating a table of values using select x values The graph of this parent quadratic is called a parabolaNOTE Any
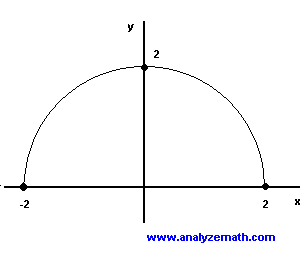



Graphing Square Root Functions
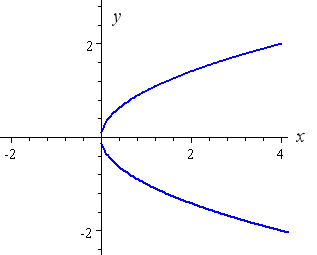



How To Draw Y 2 X 2 Interactive Mathematics
Answer choices (2,1) (2,1) (0,0) (2,1) s Question 4 SURVEY 300 seconds Q What is the axis of symmetry forGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!X^45x^24=0 \\sqrt{x1}x=7 \\left3x1\\right=4 \\log _2(x1)=\\log _3(27) 3^x=9^{x5} equationcalculator x^{2}1=0 en Related Symbolab blog posts Middl



Graphing This Circle Equation X 2 Y 2 14x 4y 0 Mathskey Com




Solved Match The Equation With Its Graph The Graphs Are Chegg Com
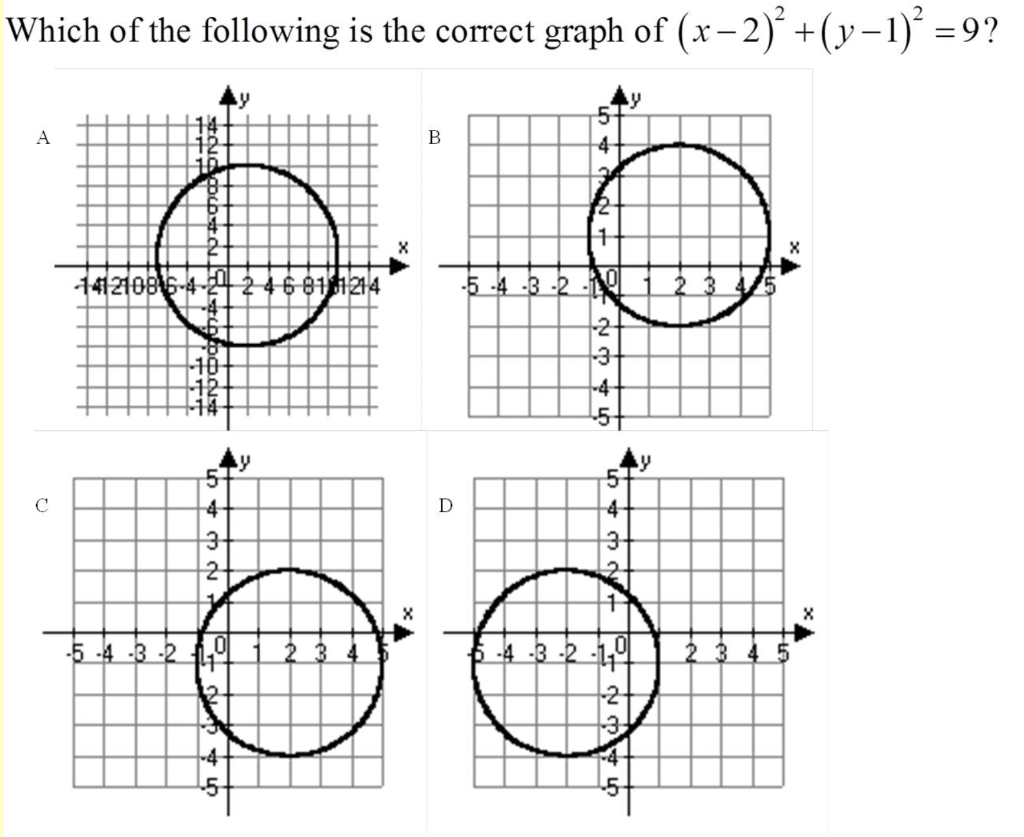



Solved Which Of The Following Is The Correct Graph Of X 2 Chegg Com
+(7x%C3%B74)+2.png)



Graph Of Y X 2 4 7x 4 2



2




Transforming Exponential Graphs Example 2 Video Khan Academy



Instructional Unit The Parabola Day 4 And 5



Graphing Quadratic Functions



Ellipses And Hyperbolae




5 07 Inverses And Their Graphs Lesson Mathspace



Surfaces Part 2




Which Of The Following Is The Graph Of X 1 2 Y 2 2 4 Brainly Com



Solution Find An Expression For The Top Half Of The Circle X 2 Y 2 2 4



Solution Graph The Ellipse And Its Foci X 2 9 Y 2 4 1




How Do You Graph Y X 1 2 4 Homeworklib




Solutions To Implicit Differentiation Problems



View Question On The Graph Of Y X 2 4 100 How Many Points Are There Whose Coordinates Are Both Negative Integers



Quadratics Graphing Parabolas Sparknotes




Sketch The Graph Of The Set X Y X2 Y2 9 Wyzant Ask An Expert



Draw The Graph Of Y X 2 4 And Hence Solve X 2 X 12 0 Sarthaks Econnect Largest Online Education Community




Absolute Value Graph And Function Review Article Khan Academy



Equation Of A Sphere Graph Physics Forums



Finding Intercepts From An Equation




3 2 Graph Linear Equations In Two Variables Mathematics Libretexts



Solution Could Someone Help Me Graph Y X 2 4




Graph Graph Inequalities With Step By Step Math Problem Solver




7 05 Rotated Conics



Image The Graph Of Equation Y 2x 2 4x 4 Equation



1




Sketch The Graph Of The Set X Y X2 Y2 9 Wyzant Ask An Expert
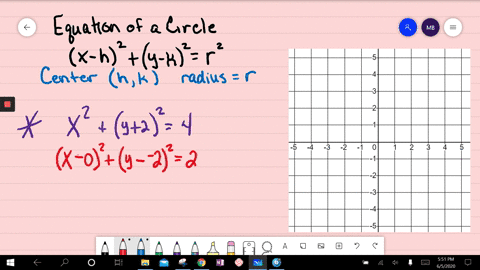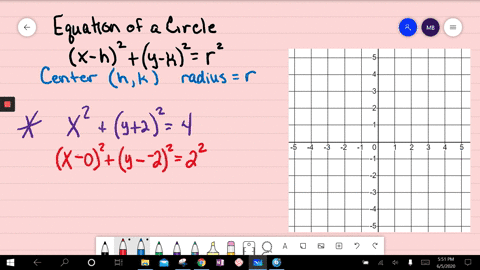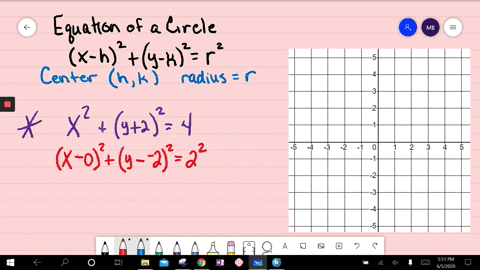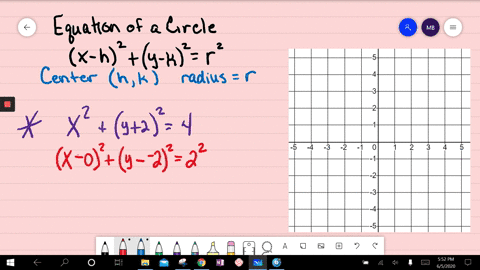



Solved Graph Each Equation X 2 Y 2 100




Graphing Sin And Cos Functions Name



How To Determine If X 2 Y 2 4 Is A Function Quora



2



The Graphs Of F X X 2 4 And G X X 2 Are Sketched Below A And B Are The X Intercepts Of F Mathrm C And Mathrm D Are The Y Intercepts Of F And G Respectively
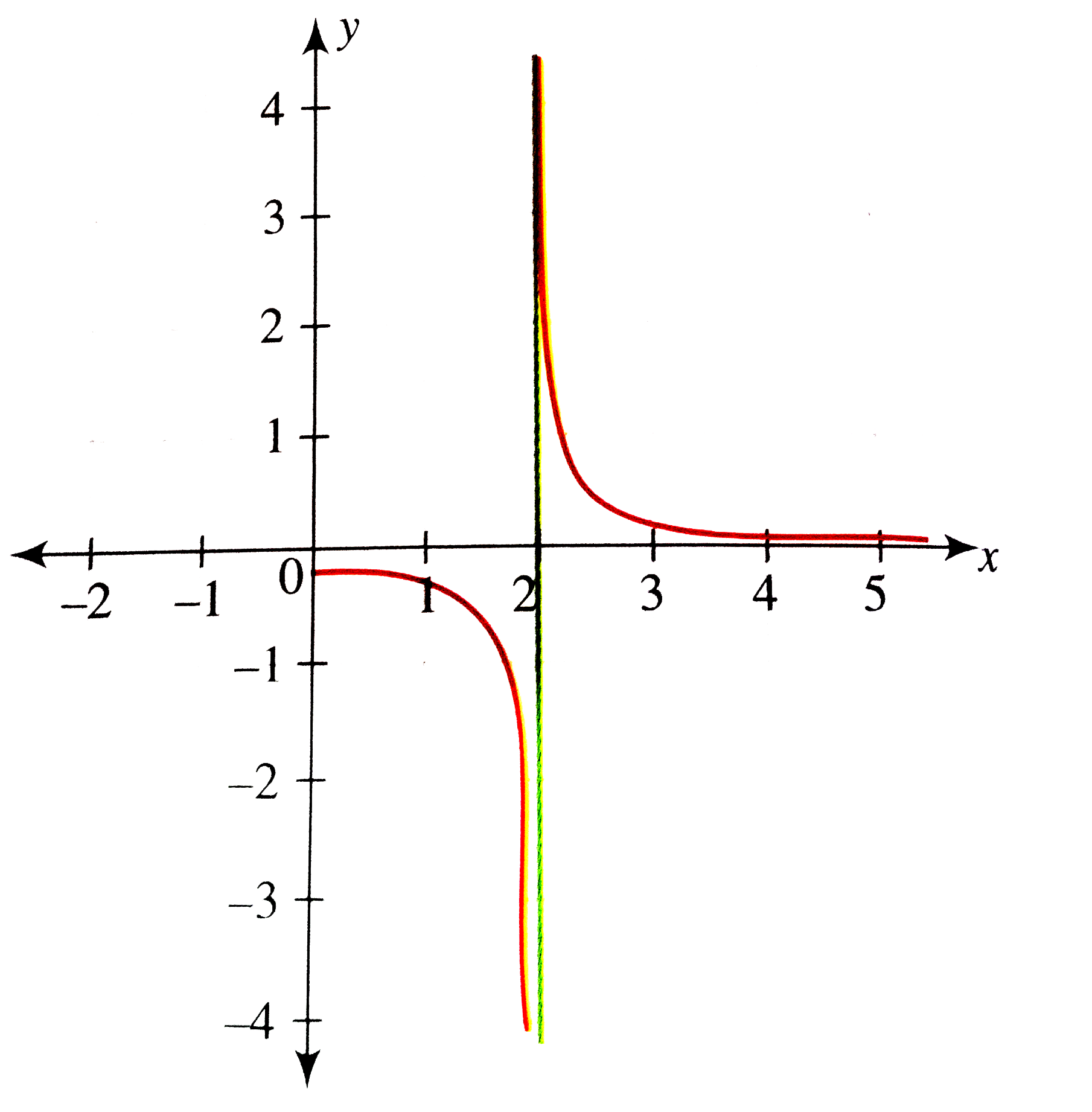



How Do I Graph The Quadratic Y 4 X 2 2 1
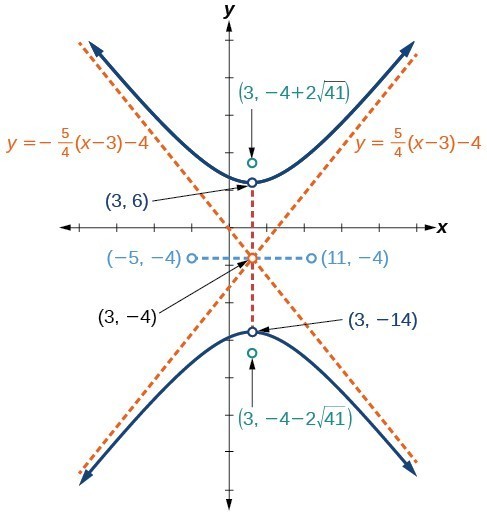



Graph Hyperbolas College Algebra



What Is The Graph Of X 2 Y 2 Z 2 1 Quora




Graph X 2 Y 2 4 Youtube




Graph The Circle X 2 Y 7 2 4 Brainly Com




Draw The Graph Of The Relation Y 2x And Using The Graph Find The Value Of Y When X 2




Surfaces Part 2
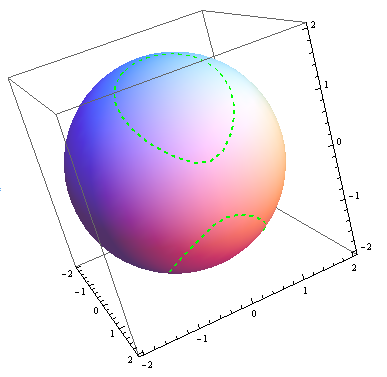



Plotting 3d Surface Intersections As 3d Curves Online Technical Discussion Groups Wolfram Community



Solved Y 2 Y 3 1 5 1 10 Y 10 Y 5 Y 3 Y 2 Y 2 0 4 4 2 X 2 4 4 2 2 X 4 2 2 4 4 O O N 2 4 2 2 4 4 2 2 X 4 2 2 Course Hero




Graph A Contour Plot With Waplot
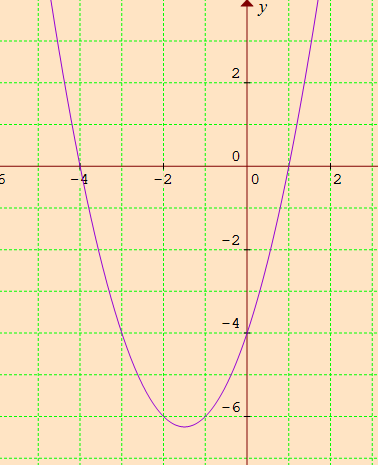



Solving Quadratic Equations By Graphing Examples




Graphing Parabolas



Key To Practice Exam 2




Graph The Region Bounded Between X Y 2 4y And X 2y Y 2 And Find The Area Study Com
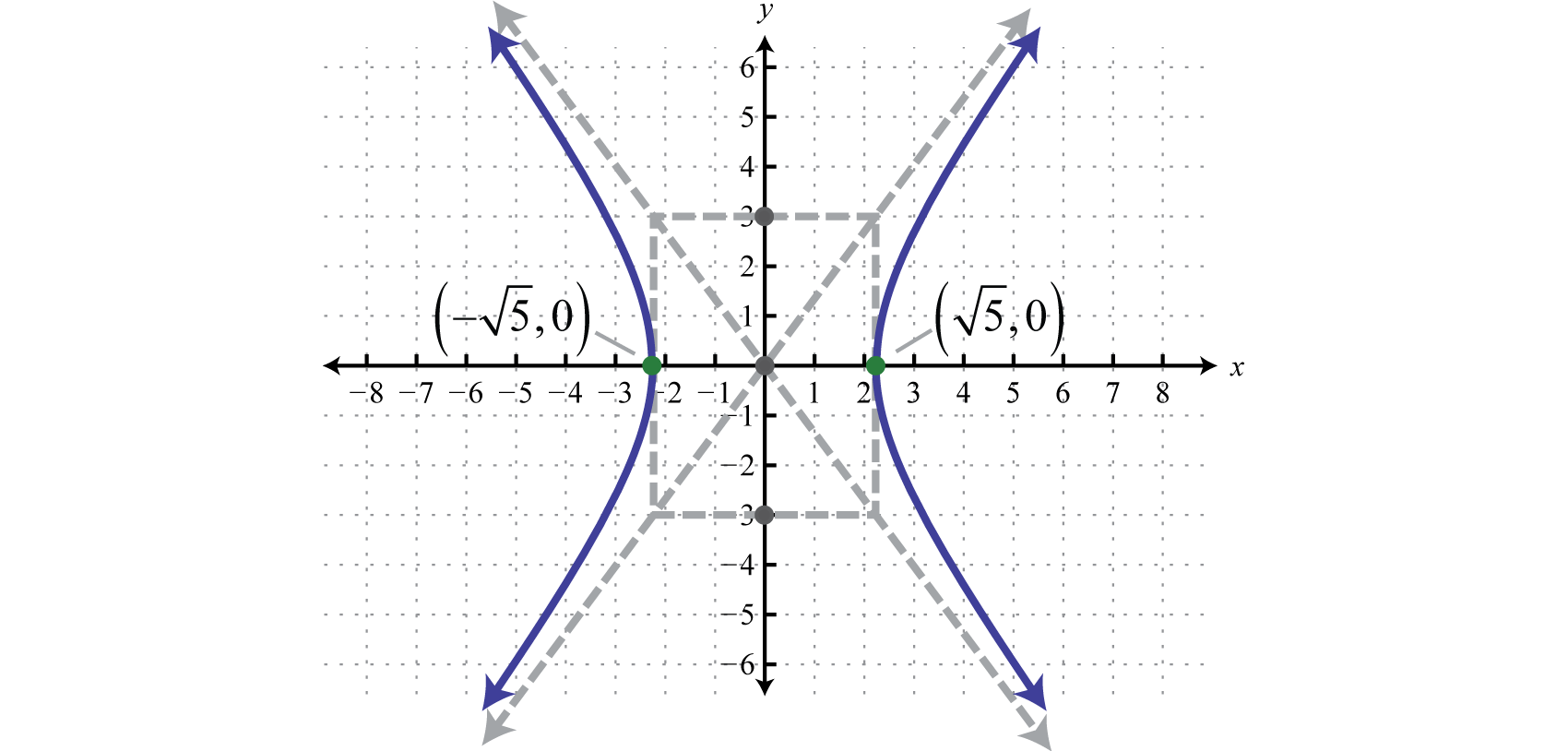



Hyperbolas



1
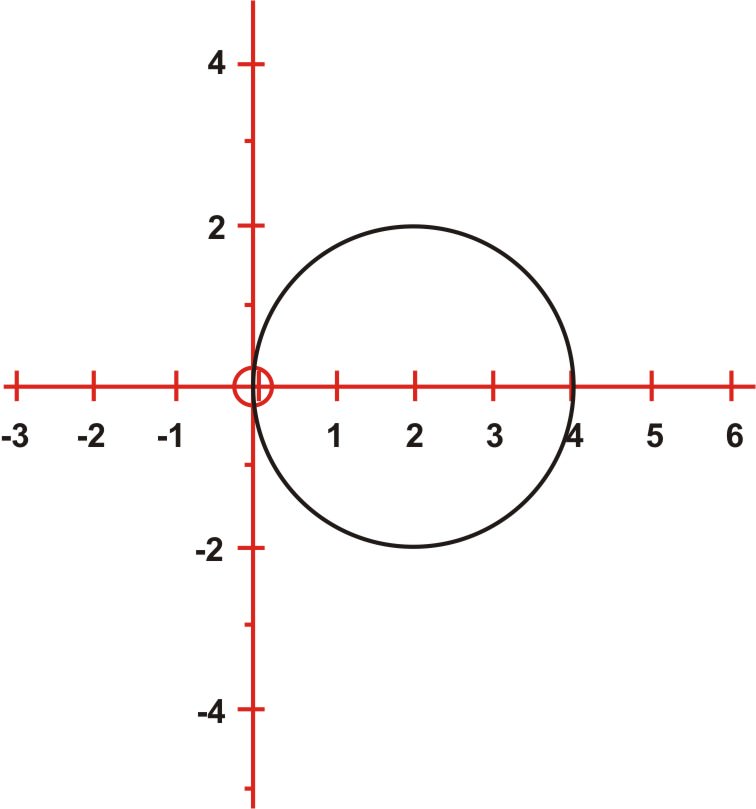



Rectangular To Polar Form For Equations Ck 12 Foundation



You Are Given That F X X 2 4 And G X X 1 Sketched In A Graph Mathsgee Answers Explanations



2




Draw The Graph Of The Surface Given By Z 1 2 Sqrt X 2 Y 2 Study Com



Solved Graph The Following Equations 2 4 Ys X 2 3 5 Course Hero




A Graph Of The Function F X Y 2x 4 4x 2 2y 4 4y 2 4 For Download Scientific Diagram



Graphing Systems Of Linear Equations



Quadricsurfaces Html
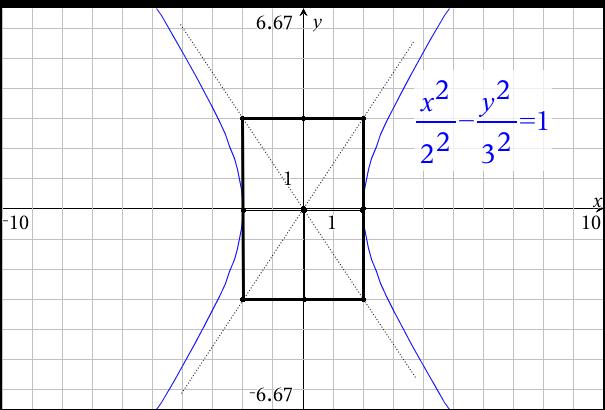



How Do You Graph X 2 4 Y 2 9 1 Socratic




How To Graph Y X 2 4 Youtube



Pplato Basic Mathematics Quadratic Functions And Their Graphs
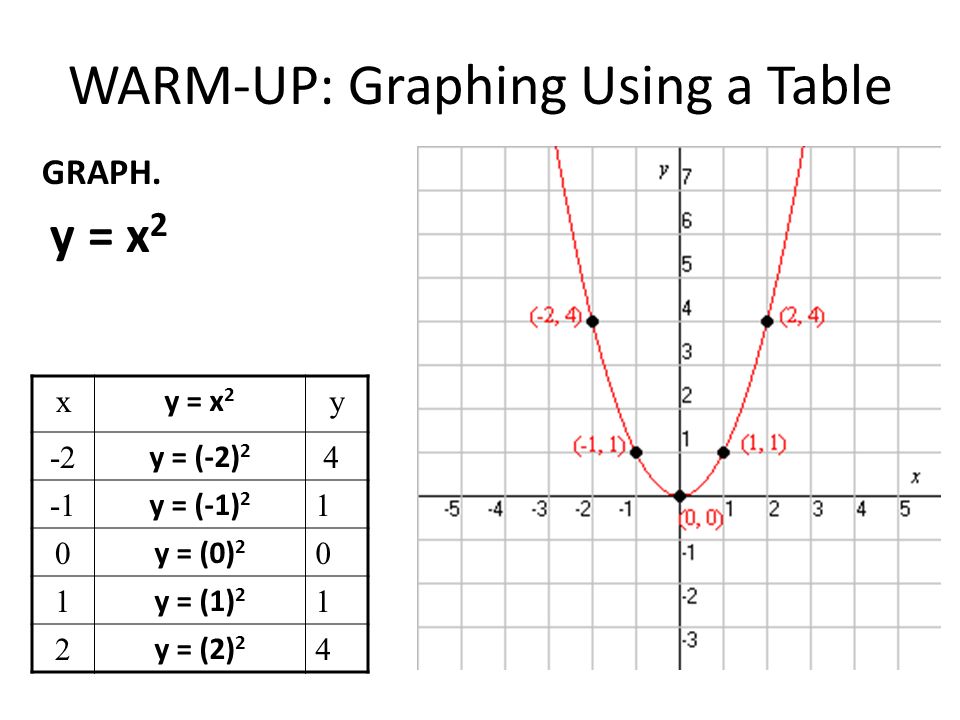



Warm Up Graphing Using A Table X Y 3x 2 Y 2 Y 3 2 2 8 Y 3 1 Y 3 0 Y 3 1 Y 3 2 2 4 Graph Y 3x Ppt Download



1
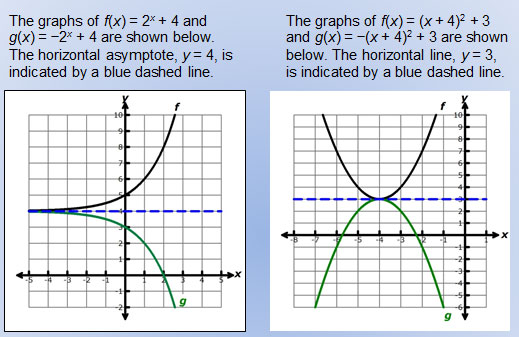



Untitled Document



Find The Foci Of The Graph Of X 2 4 Y 2 9 1 Mathskey Com



Visualizing Functions Of Several Variables And Surfaces
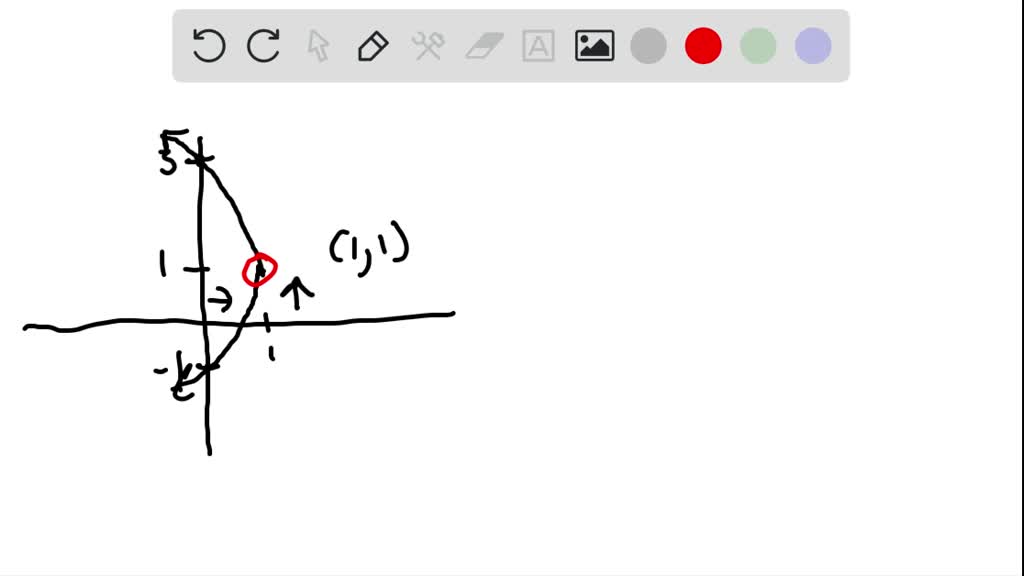



Solved The Graph Of A Parabola Is Given Match Each Graph To Its Equation A Y 2 4 X C Y 2 4 X B X 2 4 Y D X 2 4 Y E Y 1 2 4 X 1 G Y 1 2 4 X 1 F X 1 2 4 Y 1 H



Graph X 1 2 9 Y 2 2 4 1 Of Hyperbola Mathematics



Parameterized Surfaces 2 Html



14 1 Conic Sections Graphing Calculator By Mathlab User Manual




Graph The Circle X 3 2 Y 7 2 4 Brainly Com
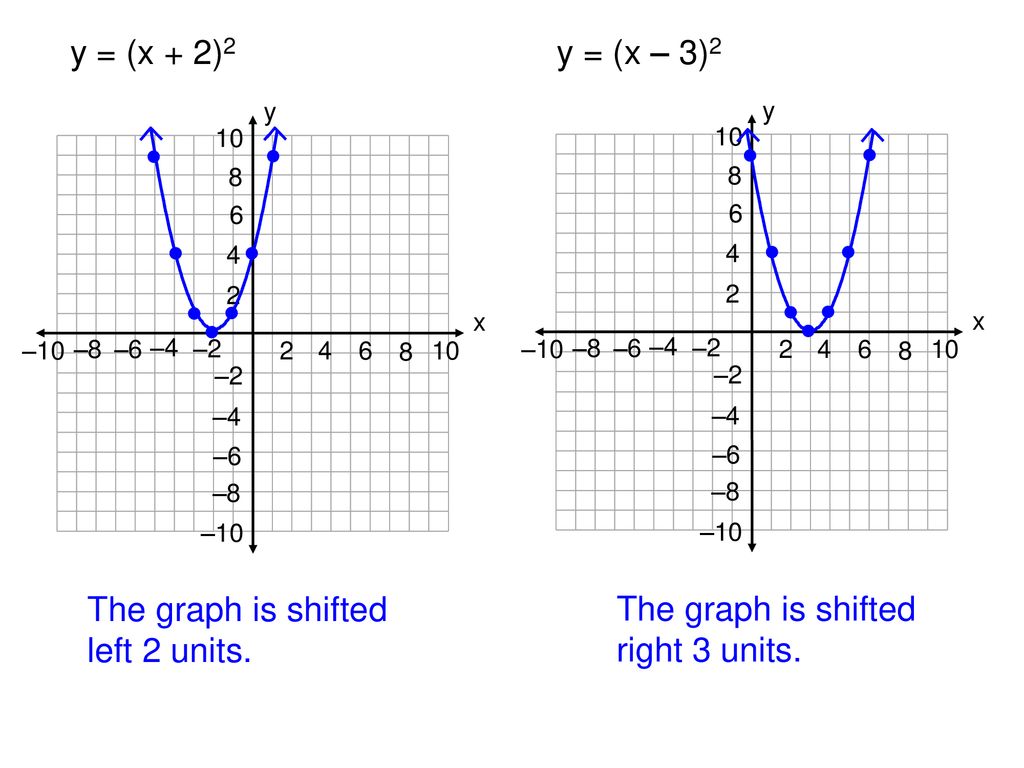



Completely Labeled Graph Ppt Download
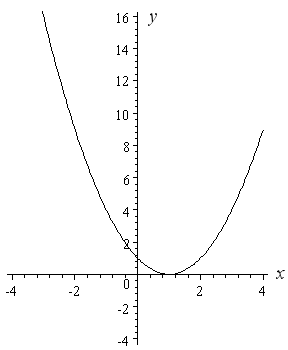



How To Draw Y 2 X 2 Interactive Mathematics




Draw The Graph Of The Equations X Y 4 And X Y 2 What Do
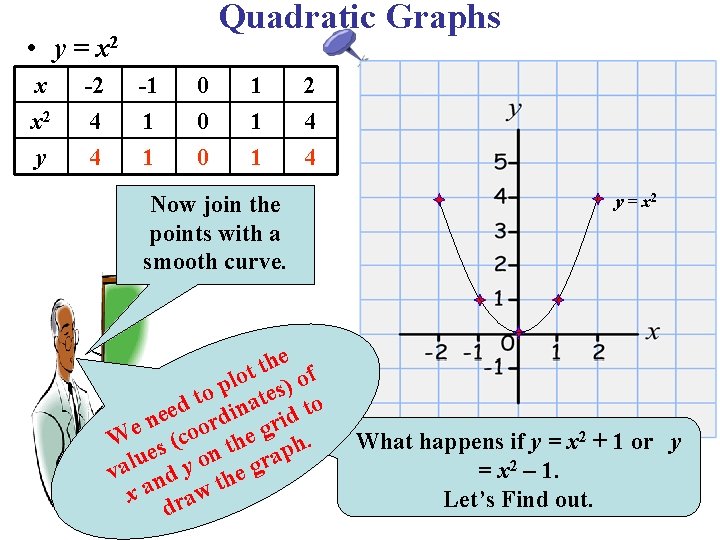



Quadratic Graphs Parabolas 1 To Draw A Quadratic




How Do You Graph X 2 Y 2 4 Socratic
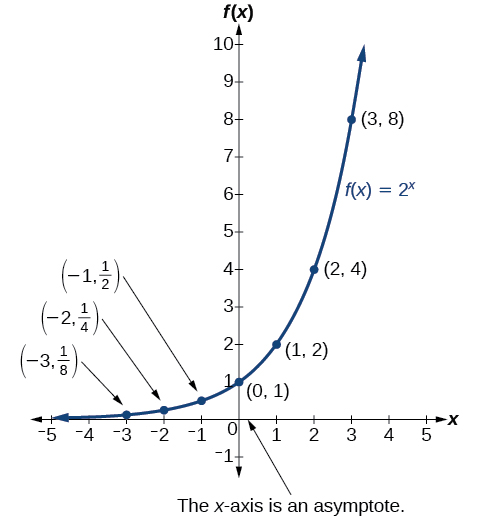



Graphs Of Exponential Functions Algebra And Trigonometry




Acute World
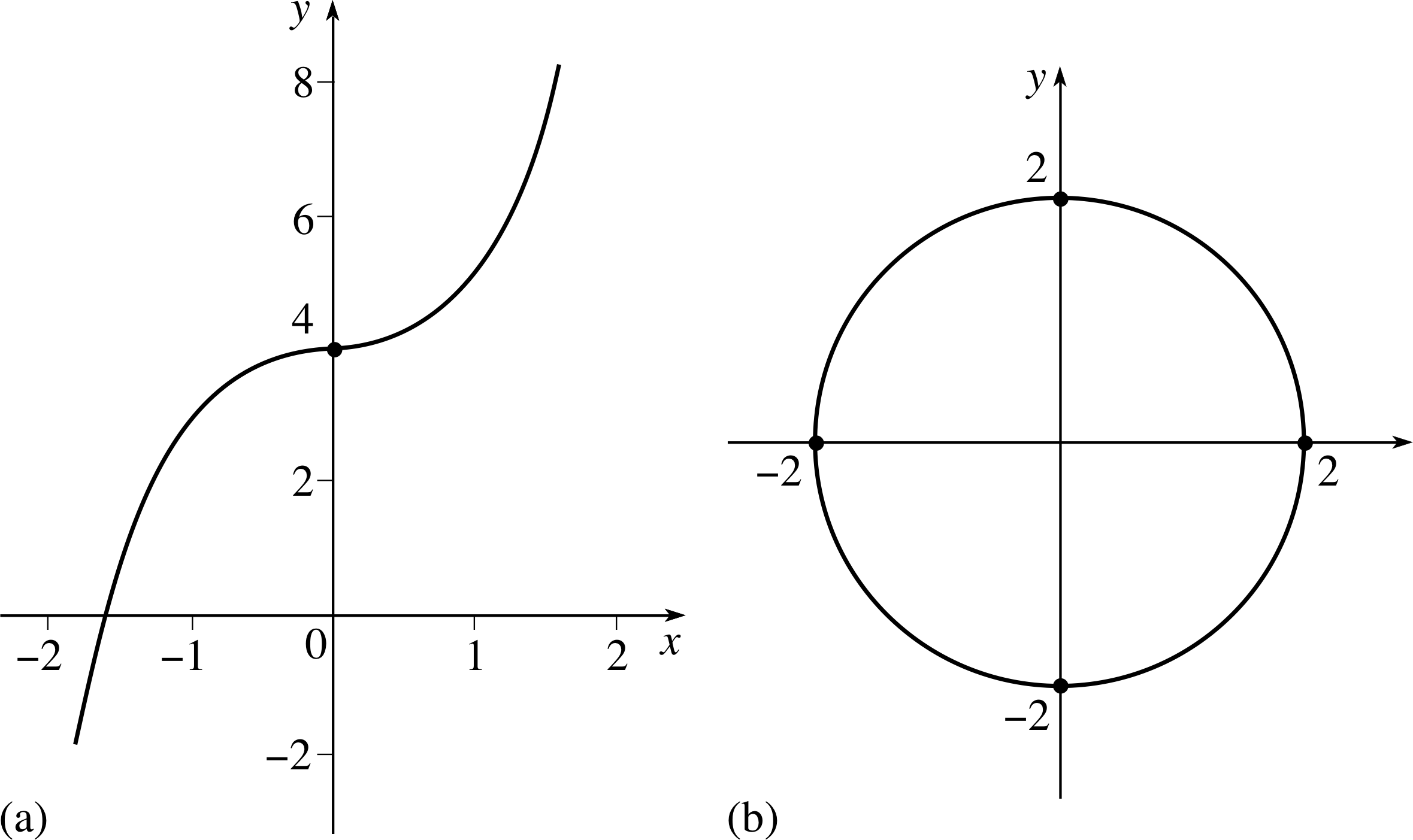



Pplato Flap Math 5 2 Basic Integration

