The equation x^2 y^2 4x 16 = 0 can be rewritten as follows This is the equation of a circle with center (2, 0) and radius sqrt You can only ask one question at a time We need to solveGraph x^2y^24x2y=0 Add to both sides of the equation Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Cancel the common factor of andYou have to change the equation to the form below (xa)^2 (yb)^2 = R^2, whereas O(a,b) is the coordinate of the center of the circle, and the R

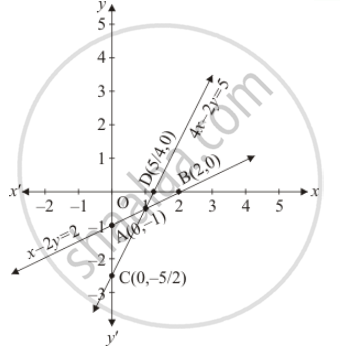
Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 Amp 4x Y 4 0 Determine The Co Ordinates Of The Vertices Of The Triangle Formed By The Lines
Graph the circle x^2+y^2+4x-6y+9=0
Graph the circle x^2+y^2+4x-6y+9=0-Answer to A circle has the equation x^{2} y^{2} 4x 4y 73 = 0 Graph the circle using the center (h,k) and radius r Find the intercepts,Graph y=x^24x2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola




Ocr Mei Core 1 3 04 Sketch The Graph Of Y X 2 4x 4 Youtube
You can put this solution on YOUR website!It's second degree in mathx/math and mathy/math so it's a conic section There's no mathxy/math cross term which means it's oriented along the axes Now we have to look hard at the coefficients on mathx^2/math and mathy^2/mathConvert the equation x^2 y^2 4x = 0 to polar coordinates Sketch the graph of r = 1 sin theta Label points Find the area of the region inside r = 1 sin theta for 0 lessthanorequalto theta lessthanorequalto pi/4
Question graph the circle x^2 y^2 4x 8y = 24 Answer by toidayma(44) (Show Source) You can put this solution on YOUR website!The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2xy^ {2}2y=0 x 2 2 x y 2 2 y = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2 for b, and y\left (2y\right) for c in the quadratic formula, \frac {The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction y^ {2}2yx^ {2}4x=0 y 2 2 y x 2 − 4 x = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2 for b, and x\left (4x\right) for c in the quadratic formula, \frac {
The equation is x 2 y 2 4x 6y 3 = 0 Compare the above equation with Ax 2 Bxy Cy 2 Dx Ey F = 0 A = 1 and C = 1 Since, A and C have opposite signs The given equation represents the curve hyperbola Write the equation x 2 y 2 4x 6y 3 = 0 in standard form of hyperbola x 2 y 2 4x 6y 3 = 0 x 2 4x 3Graph x^24y^24x=0 Find the standard form of the hyperbola Tap for more steps Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute the values of and into the formula Simplify the right side Explanation From the given equation x2 y2 2x −3 = 0 perform completing the square method to determine if its a circle, ellipse, hyperbola There are 2 second degree terms so we are sure it is not parabola x2 y2 2x −3 = 0 x2 2x y2 = 3 add 1
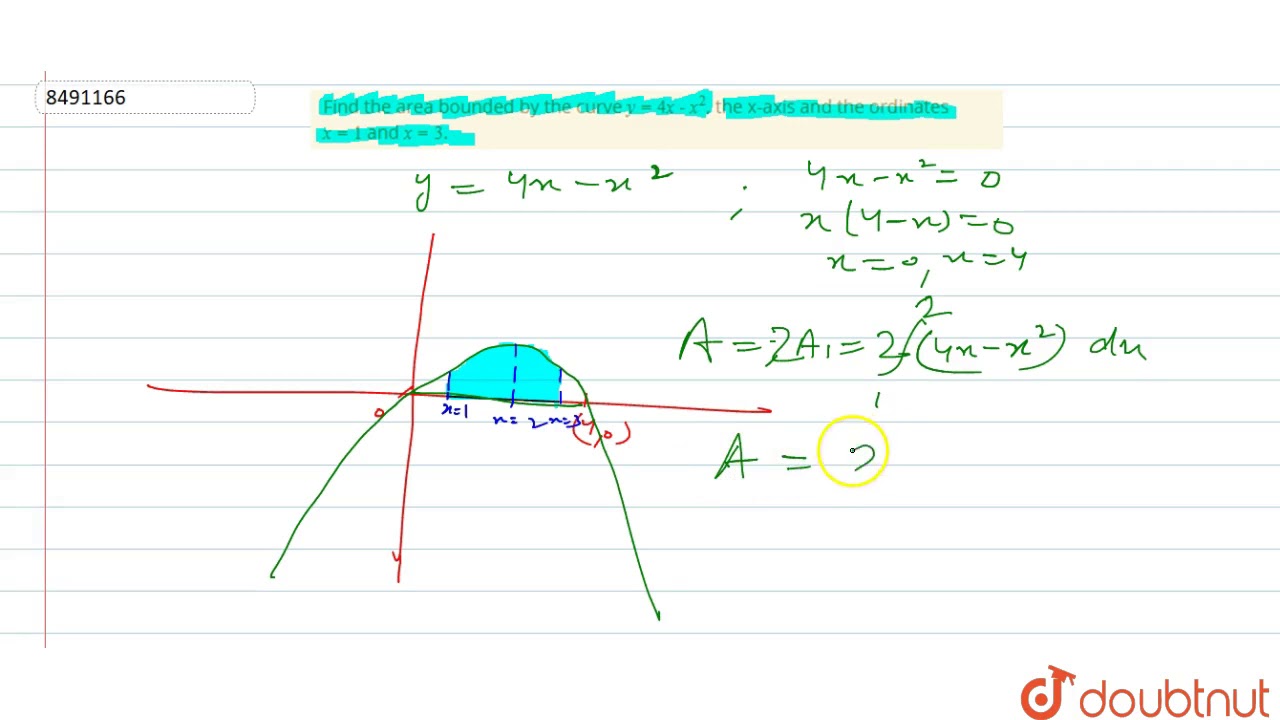



Find The Area Bounded By The Curve Y 4x X 2 The X Axis And The Ordinates X 1 And X 3 Youtube




Draw The Graphs Representing The Equation 2x Y 2 And 4x 3y 24 On The Same Graph Paper Find The Brainly In
Algebra > Circles> SOLUTION Graph the Circle x^2y^24x2y=0 I get (x^24x)(y^22y)= (x^24x4)(y^22y1)=164 (x2)^(y1)^2=(40/2)^2 But I don't think its right can you help me with wha Log On Geometry Circles and their properties Geometry Solvers SolversThe quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}4xy^ {2}4y6=0 x 2 − 4 x y 2 − 4 y 6 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 4 for b, and y^ {2}4y6 for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} Given the equation x ^ 2 y ^ 2 4x 6y 9 = 0 A find the center and radius B find the intercepts Change Submitted 10 years ago Category Math Homework
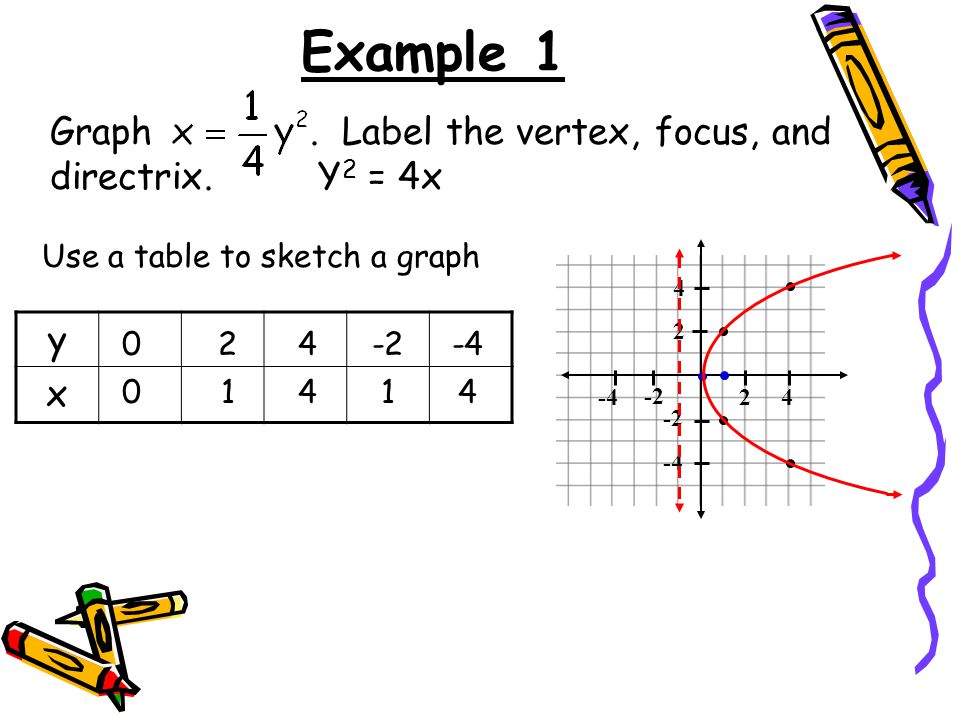



8 2 Graph And Write Equations Of Parabolas Ppt Download



Graphing This Circle Equation X 2 Y 2 14x 4y 0 Mathskey Com
X^2 y^2= 4x There is a horizontal tangent at the point(s) Question At what point(s) does the graph of the function shown below have a horizontal tangent?Substitute (x−2)2 − 4 ( x 2) 2 4 for x2 −4x x 2 4 x in the equation x2 y2 −4x = 0 x 2 y 2 4 x = 0 Move −4 4 to the right side of the equation by adding 4 4 to both sides Add 0 0 and 4 4 This is the form of a circle Use this form to determine the center and radius of the circle To find its coordinates and radius you should transform it to form of (xa)^2(yb)^2=r^2 (1) We start from the equation given x^2y^24x2y4=0 Now we can group terms with the same variable x^24xy^22y4=0 Now we can complete the squares of variables x^24x color(red)(4) y^22y color(red)(1) color(red)(5) 4=0 I added 5 so I had to substract 5 to




The Area Bounded By The Parabola Y 4x 2 Y X 2 9 And The Li



Solution Graph Y 2x 2 4x
I'm so confused, please help!This problem has been solved! This is the equation of a circle centre (2, 2) and radius 3 >0 = x^2y^24x4y1 = (x^24x4)(y^24y4)9 = (x2)^2(y2)^23^2 Add 3^2 to both ends and transpose to get (x(2))^2(y2)^2 = 3^2 This is in the form (xh)^2 (yk)^2 = r^2 the standard form of the equation of a circle with centre (h, k) = (2, 2) and radius r=3 graph{(x^2y^24x4y1)((x2)^2(y2)^2
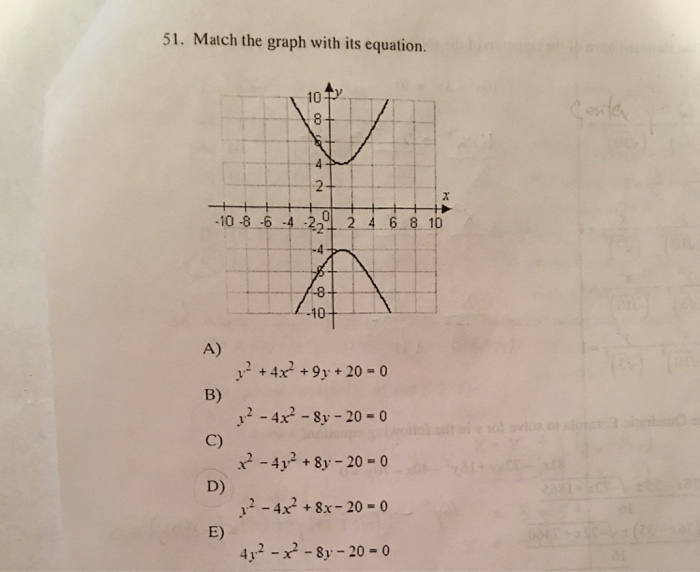



Match The Graph With Its Equation Y 2 4x 2 9y Chegg Com
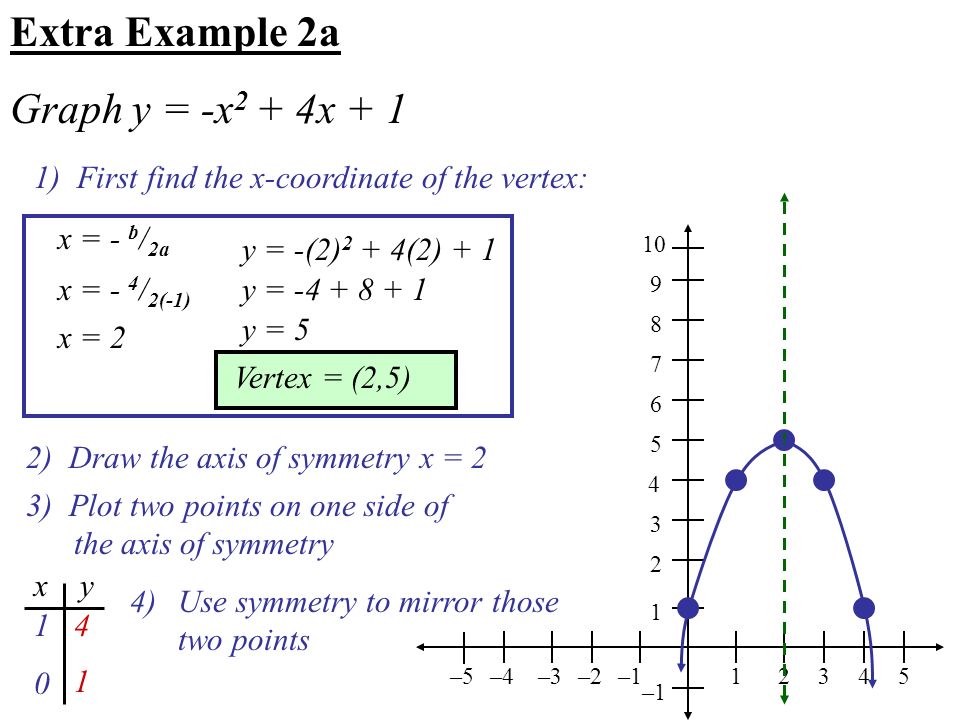



Ch 5 Notes Ppt Video Online Download
A circle has the equation of x^2y^24x4y73=0 Graph the circle using the center (h,k) and radius r Find the intercepts, if any, of the graphI've been racking my brain for the last minutes over this problem!Divide 42\sqrt{\left(6y\right)y} by 2 x=\sqrt{y\left(y6\right)}2 x=\sqrt{y\left(y6\right)}2 The equation is now solved x^{2}4xy^{2}6y4=0 Quadratic equations such as this one can be solved by completing the square In order to complete the square, the equation must first be in the form x^{2}bx=c




Sketch The Graph Of The Function F X Y Sqrt 4x 2 Y 2 Study Com




Graph Of Y 4x Novocom Top
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Algebra > Graphs> SOLUTION Find the center and radius of the circle given by the equation x^2y^24x4y−28=0 Log On Algebra Graphs, graphing equations and inequalities Section Solvers SolversThe graph of y^2=4x represents a graph of a quadratic function On the given graph you can find all of the important points for function y^2=4x (if they exist) You can always share this solution



How Do You Graph X 2 Y 2 9 And What Are Its Lines Of Symmetry Socratic




Draw The Graph Of The Following Equations 2x Y 2 0 4x 3y 24 0 Y 4 0 Obtain The Vertices Of The Triangle So Obtained Also Determine Its Area Snapsolve
Simple and best practice solution for x^24xy^212y=32 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itA circle is all points in a plane that are a fixed distance from a given point on the plane The given point is called the center, and the fixed distance is called the radius The standard form of the equation of a circle with center (h,k) ( h, k) and radius r r is (x−h)2(y−k)2 = r2 (The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}4xy^ {2}4y8=0 x 2 4 x y 2 4 y 8 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 4 for b, and y^ {2}4y8 for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}




Graph The Parabola Y X 2 4x 1 Youtube




Graphing Parabolas
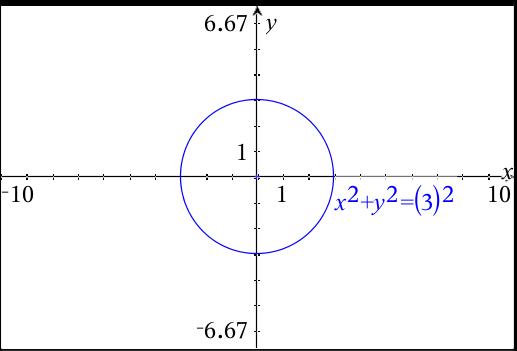
Steps to graph x^2 y^2 = 4What is the area of the following circle x^2y^24x6y12=0? (x2)^24 (y 2)^24 = 1 Leading to (x2)^24 (y 2)^2 = 9 (x2)^24 (y 2)^2 = 3^2 Which if we compare to the standard equations of the conics represents circle of radius 3 centred at (2,2) graph{x^2 y^2 4x 4y 1 = 0 926, 4784, 127, 575}



Solution Can You Graph The Equation Y X 2 4x 5 If You Can Please Explan How U Got The Vertex And How To Graph Everything Thanks



Solution Graph The Circle X 2 Y 2 4x 10y 0
Simple and best practice solution for X^2y^24x6y23=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkGraph x^2y^2=4 x2 − y2 = 4 x 2 y 2 = 4 Find the standard form of the hyperbola Tap for more steps Divide each term by 4 4 to make the right side equal to one x 2 4 − y 2 4 = 4 4 x 2 4 y 2 4 = 4 4 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of an ellipse or hyperbola requiresMathz=\sqrt{4x^2y^2}\iff x^2y^2z^2=4\,,\,z\geq0/math This is the top half of a sphere of radius 2, centered at the origin



1




The Graph Of Y 4x Tex X 2 Tex 4x 1 Is Shown Brainly Com
Example 2 y = x 2 − 2 The only difference with the first graph that I drew (y = x 2) and this one (y = x 2 − 2) is the "minus 2" The "minus 2" means that all the yvalues for the graph need to be moved down by 2 units So we just take our first curve and move it down 2 units Our new curve's vertex is at −2 on the yaxisGraph y^2=4x y2 = 4x y 2 = 4 x Rewrite the equation as 4x = y2 4 x = y 2 4x = y2 4 x = y 2 Divide each term by 4 4 and simplify Tap for more steps Divide each term in 4 x = y 2 4 x = y 2 by 4 4 4 x 4 = y 2 4 4 x 4 = y 2 4 Cancel the common factor of 4 4Y=x^24x4 (graph 300x0 pixels, x from 6 to 5, y from 10 to 10, x^2 4x 4) Intercepts (0,4) (2,0) Proof using the (2,0) x & y values 0=2^24*24 0=484 0=0 Answer by ewatrrr () ( Show Source )
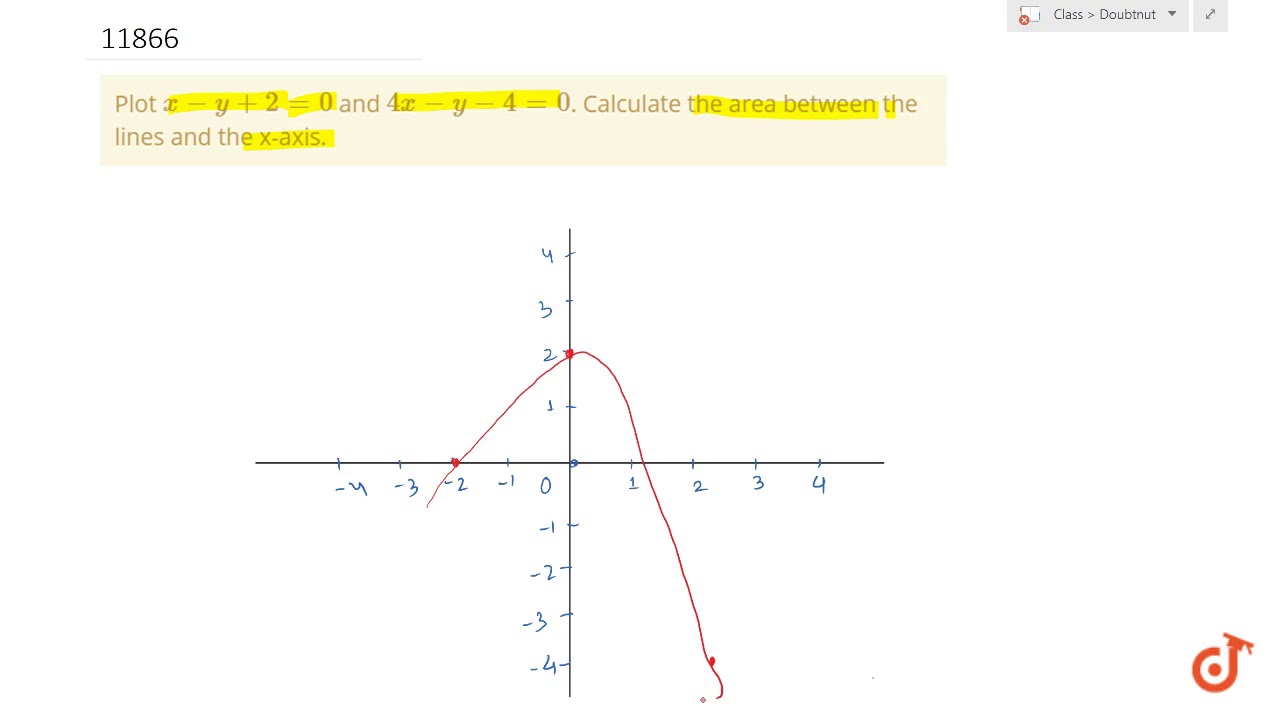



Plot X Y 2 0 And 4x Y 4 0 Calculate The Area Between The Lines And The X Axis Youtube




Y X 2 Y 0 X 4 Novocom Top
X^2y^24x8y5=0 x^2y^24x8y5=0 completing the square (x^24x4) (y^28y16)=0416= Equation (x2)^2 (y4)^2= This is a circle with center at (2/4) with a radius of sqrt ()=447 see graph belowAnalysis The well known formula for the area of a circle is ( pi )r² To use this formula we need to know the value of the radius " r " From the standard (General Equation) of a circle,3)y=x^24x •Graph this original function in its entire domain but coloring green that portion of the graph over the limited domain x>=2, •Find its inverse over x>=4, •On another set of coordinate axes, graph this inverse Color it blue



Determine Graphically Whether The System Of Equations X 2y 2 4x 2y 5 Is Consistent Or In Consistent Mathematics Shaalaa Com
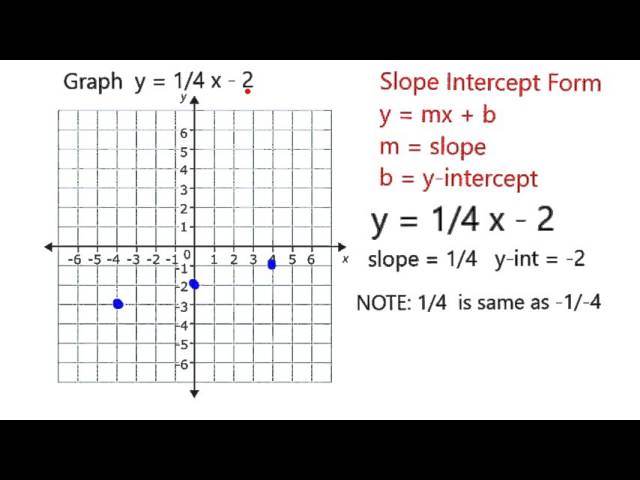



Graph Y 1 4 X 2 Youtube
X²y²4x6y = 3 We can write this equation as x²4x4 y²6y9–4–9 = 3 (x2)²(y3)² = 16 Now campare this equation with standard circle equation Which is (xh)²(yk)² = r² Where r is radius and center is (h,k) Now, We will find the centre and rSimple and best practice solution for x^2y^24x10y29=36 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itWhen you complete the square in x and y , you get X^2 4x 4 y^2 6y 9 = 12 4 9 = 25 And (x 2)^2 (y 3)^2 = 25 or 5^2 So the radius is 5 and the center is at (‐2, 3) So the height of the triangle is 3 and the two sides are the



Exploration Of Parabolas
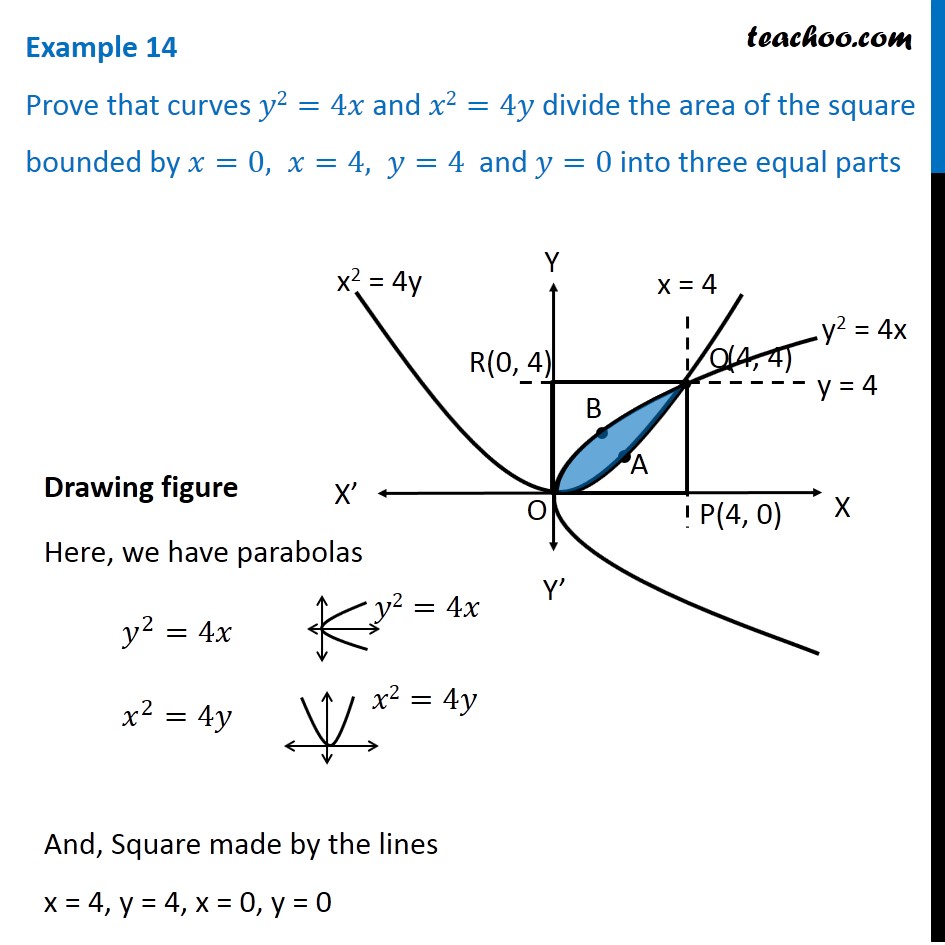



Example 14 Prove That Y2 4x X2 4y Divide Area Of Square
It is a linear equation So it is in this formy=mxb Here, 'm' is the slope and c is the 'y' intercept We see a ()sign before 4 so it is a linear equationSin (x)cos (y)=05 2x−3y=1 cos (x^2)=y (x−3) (x3)=y^2 y=x^2 If you don't include an equals sign, it will assume you mean " =0 " It has not been well tested, so have fun with it, but don't trust it If it gives you problems, let me know Note it may take a few seconds to finish, because it has to do lots of calculationsThe quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}4xy^ {2}2y2=0 x 2 4 x y 2 − 2 y 2 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 4 for b, and y^ {2}2y2 for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}
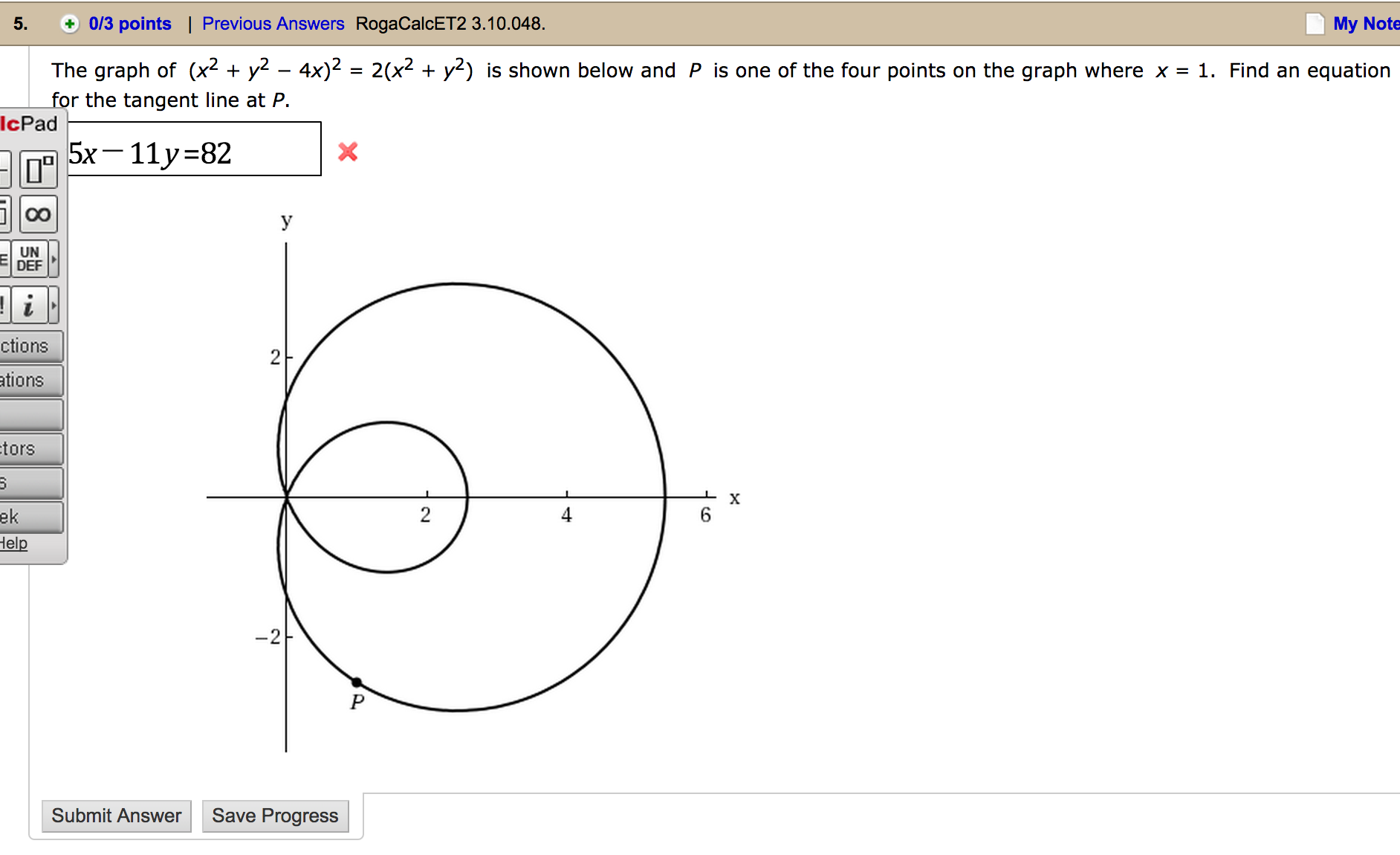



The Graph Of X2 Y2 4x 2 2 X2 Y2 Is Shown Chegg Com



How To Graph A Parabola Y 4x 2 Socratic
I've completely spaced out how to set this problem up!Question What is the vertex of the graph y = x^2 4x 12 ?



Solution Graph F X X 2 4x 3 Labeling The Y Intercept Vertex And Axis Of Symmetry




Plot A Graph For The Equation Y X 2 4x




The Graph Of Y X2 4x Is Shown On The Grid By Drawing The Line Y X 4 Solve The Equations Y Brainly Com



What Is The Area Of The Following Circle X 2 Y 2 4x 6y 12 0 Quora




Traces Of The Level Surface Z 4x 2 Y 2 Mathematica Stack Exchange



How Do I Graph The Quadratic Equation Y X 2 4x 6 Socratic



What Is The Area Bounded By The Curve Y 4x X And The Lines X 0 And Y 4 Quora



What Is The Vertex Of Y X 2 4x 1 Socratic




Draw The Graphs Of The Pair Of Linear Equations X Y 2 0 Amp 4x Y 4 0 Determine The Co Ordinates Of The Vertices Of The Triangle Formed By The Lines
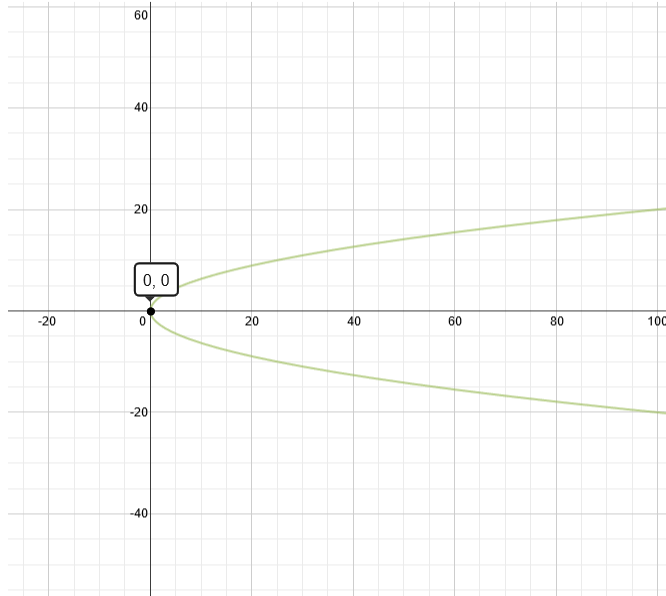



Graph Of Y 2 4x




The Graph Of Y X 2 4x 3 Is Shown A What Are The Coordinates Of The Turning Point B What Are Brainly Com



35 Reduce The Equation X 2 Y 2 Z 2 4x 2y 2z 4 0 To One Of The Standard Forms Classify The Surface And Sketch It Toughstem



Solution Graph The Parabola Y X2 4x 4 Use The Quadratic Formula To Solve The Equation To The Exact Value Or Round To Two Decimal Places 2x 2 X 1
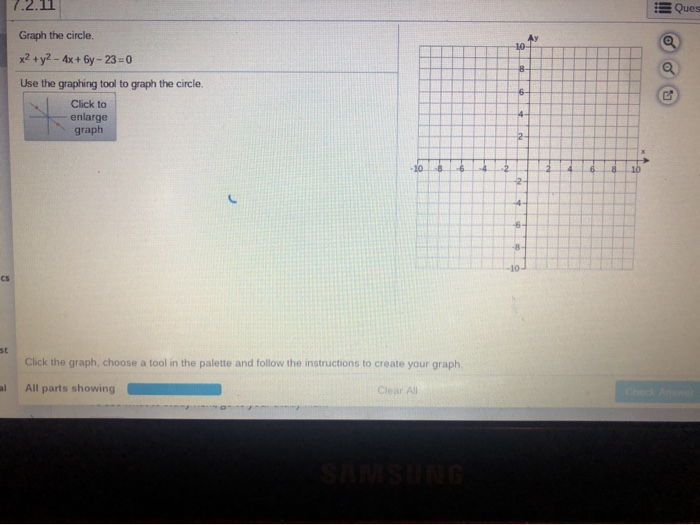



1 2 11 Graph The Circle X2 Y2 4x 6y 23 0 Use Chegg Com



Content Transformations Of The Parabola



Parabolas




Ex 8 2 7 Area Lying Between Y2 4x And Y 2x Is Ex 8 2




4 X 2 2x Y 2 8 4 Example 6 Classify A Conic Classify The Conic Given By 4x 2 Y 2 8x 8 0 Then Graph The Equation Solution Note Ppt Download




Quadratic Polynomial Y X 2 4x 4 Draw A Graph And Represent The Zeroes Of The Polynomial
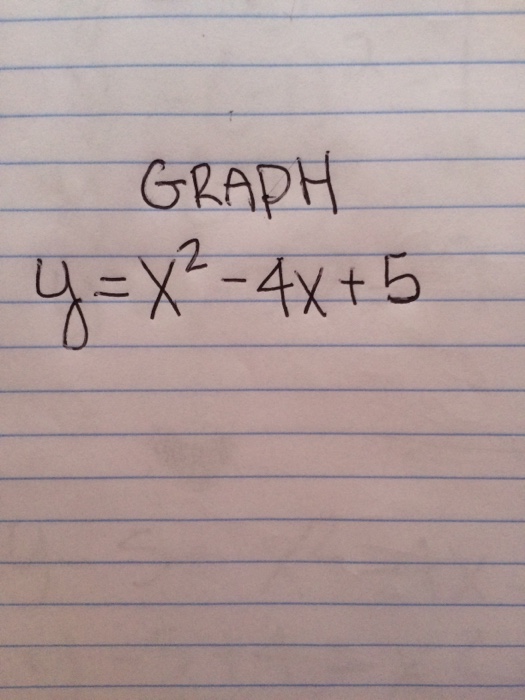



Graph Y X 2 4x 5 Chegg Com



1



What Is The Graph Of X 2 Y 2 Z 2 1 Quora




Solution The Equation X 2 Y 2 4x 2y 0 Describes



How To Graph Math Y 6x 2 2x Math Quora



Exploration Of Parabolas
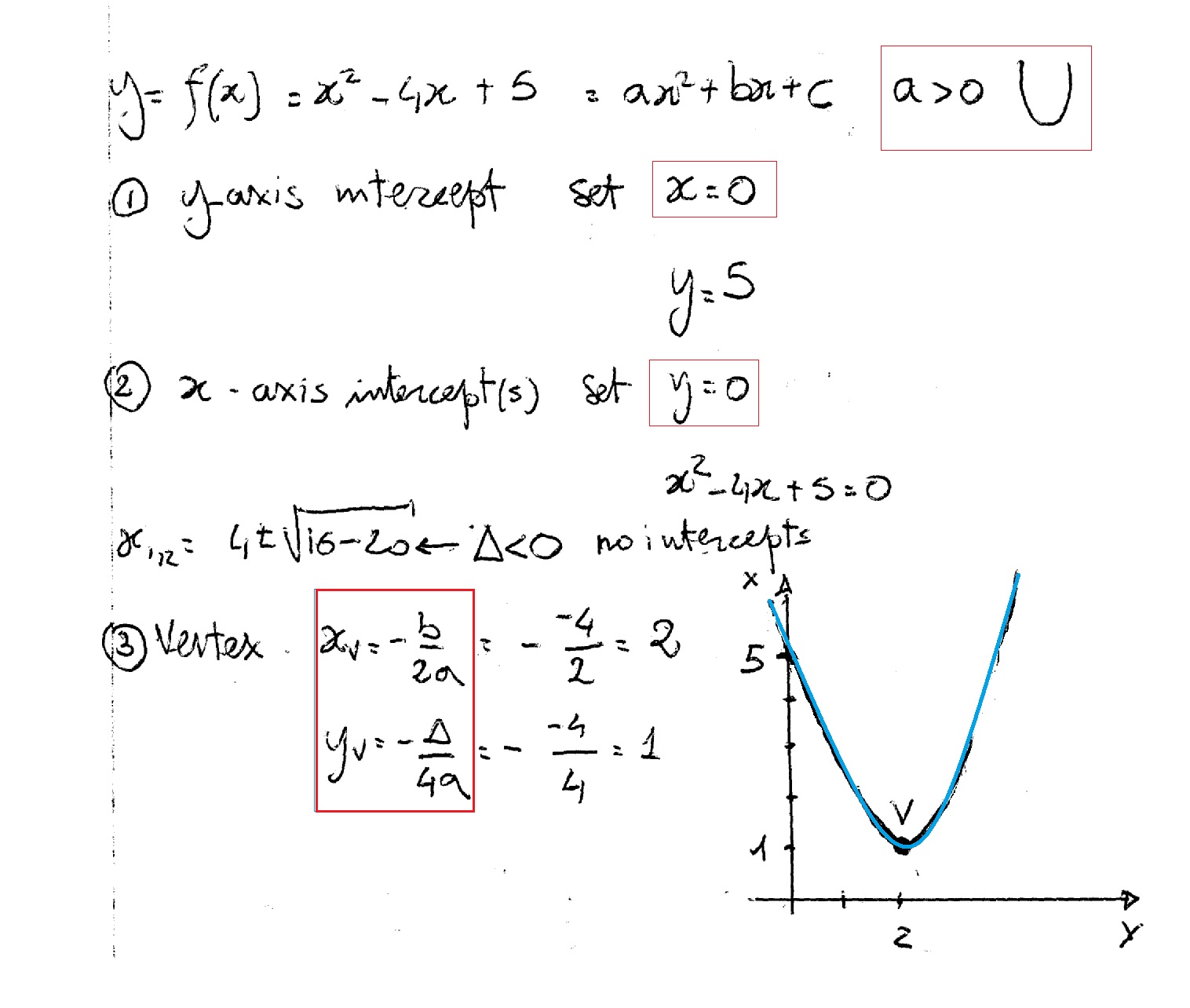



How Do You Graph F X X 2 4x 5 Socratic




How Do You Graph Quadratic Functions Y X 2 4x 7 Socratic




Graphing Quadratic Functions Rational Functions Conic Sections Ppt Download



Find The Area Of The Region Bounded By The Curve Y2 2x And X2 Y2 4x Studyrankersonline
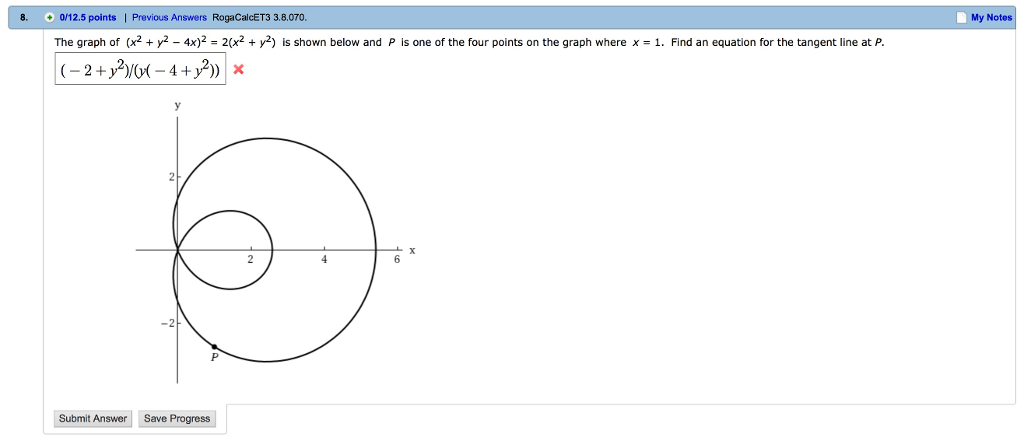



The Graph Of X2 Y2 4x 2 2 X2 Y2 Is Chegg Com




The Graph Of Y Sqrt 4x X 2 Is Given Use Transformations To Create A Function Whose Graph Is As Shown Below Study Com




How To Draw Y 2 X 2




Draw The Graphs Representing The Equation 2x Y 2 And 4x 3y 24 On The Same Graph Paper Find The Brainly In
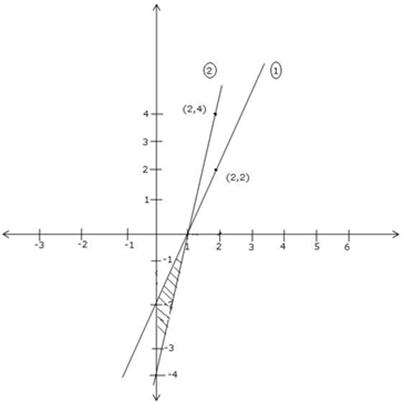



Solve Graphically 2x Y 2 And 4x Y 4 Shade The Region Between These Lines And The Y Axis Mathematics Topperlearning Com 2kj2s63hh



1




Ocr Mei Core 1 3 04 Sketch The Graph Of Y X 2 4x 4 Youtube



Solution 2 For The Function Y X2 4x 5 Perform The Following Tasks A Put The Function In The Form Y A X H 2 K Answer Show



Identify The Equation Of The Following Graph Select Chegg Com



Solution Write The Parabola In Standard Form And Graph X 2 4y 28 0 Write The Ellipse In Standard Form And Graph 2x 2 Y 2 4x 4y 4 0 Write The Hyperbola In Standard Form And Graph X 2




How To Draw Y 2 X 2
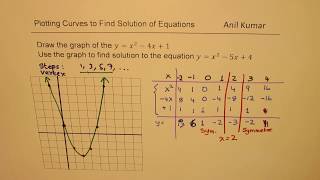



Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube




What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora




5 3 The Graphs Of Quadratic Equations X
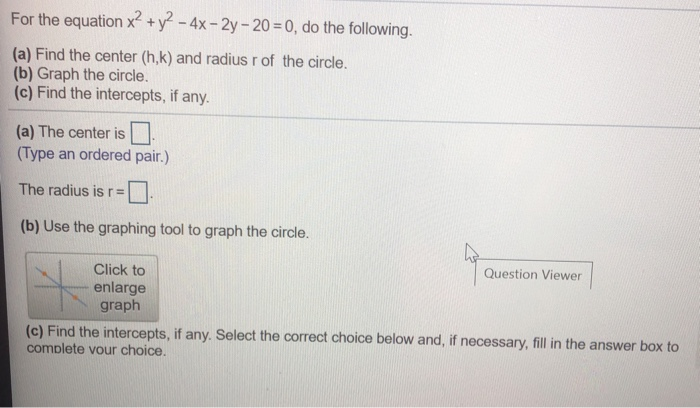



For The Equation X2 Y2 4x 2y 0 Do The Chegg Com




Misc 15 Find Area X Y Y2 4x 4x2 4y2 9 Miscellaneous



Solution I Need To Graph This Circle X 2 Y 2 4x 8y 5 0



How To Draw Y 2 X 2



Ellipses And Hyperbolae
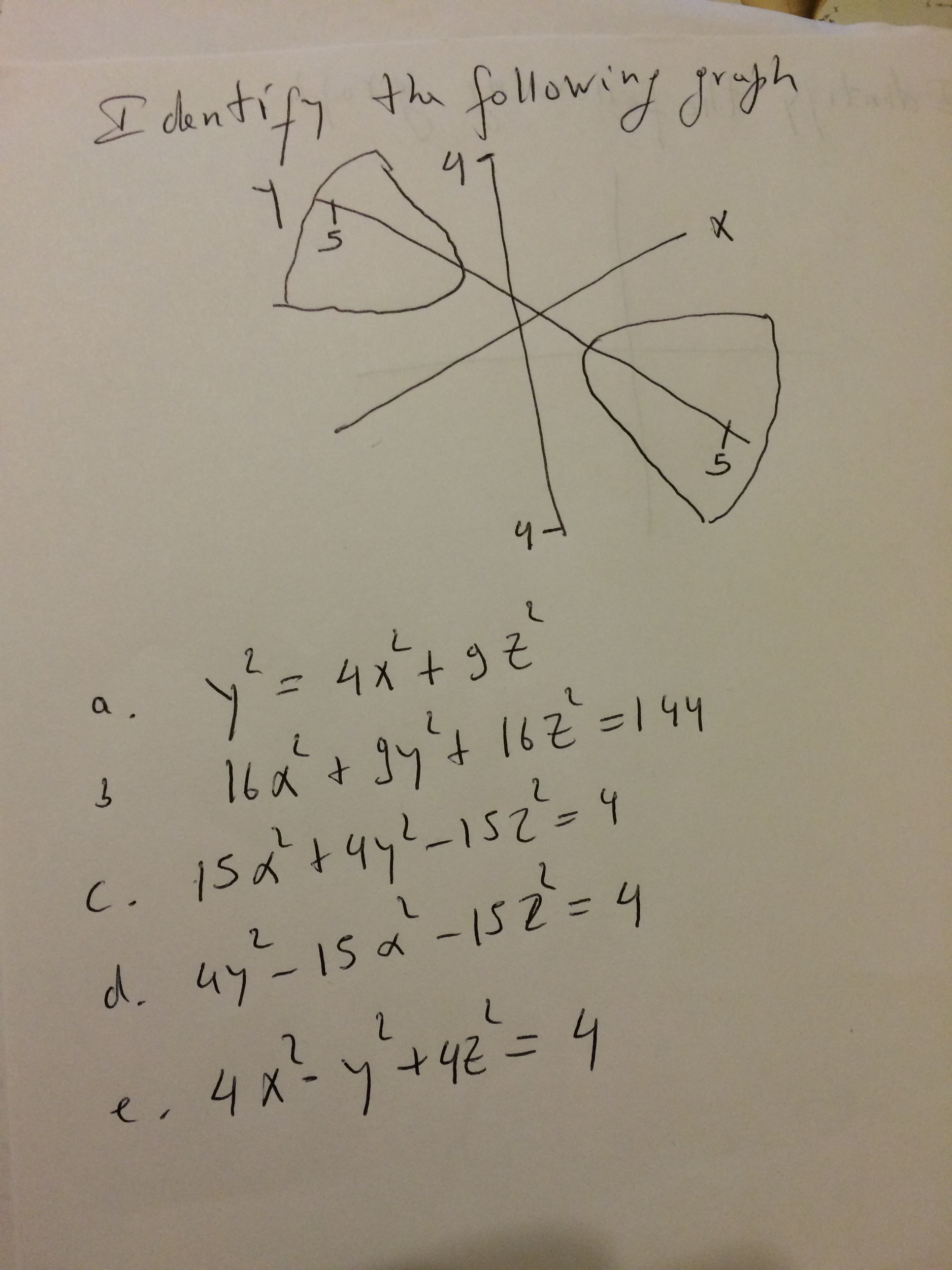



Identify The Following Graph A Y 2 4x 2 Gz 2 B Chegg Com




Rough Sketch Of The Circle X 2 Y 2 8x And The Parabola Y 2 4x Mathematics Stack Exchange




How Do You Graph X 2 Y 2 4 Socratic



Graphing Quadratic Functions



How To Represent The Graph Of The Parabola Y 2 4x Quora



Solution Graph The Parabola Y 2x 2 4x 6 On Graph Paper
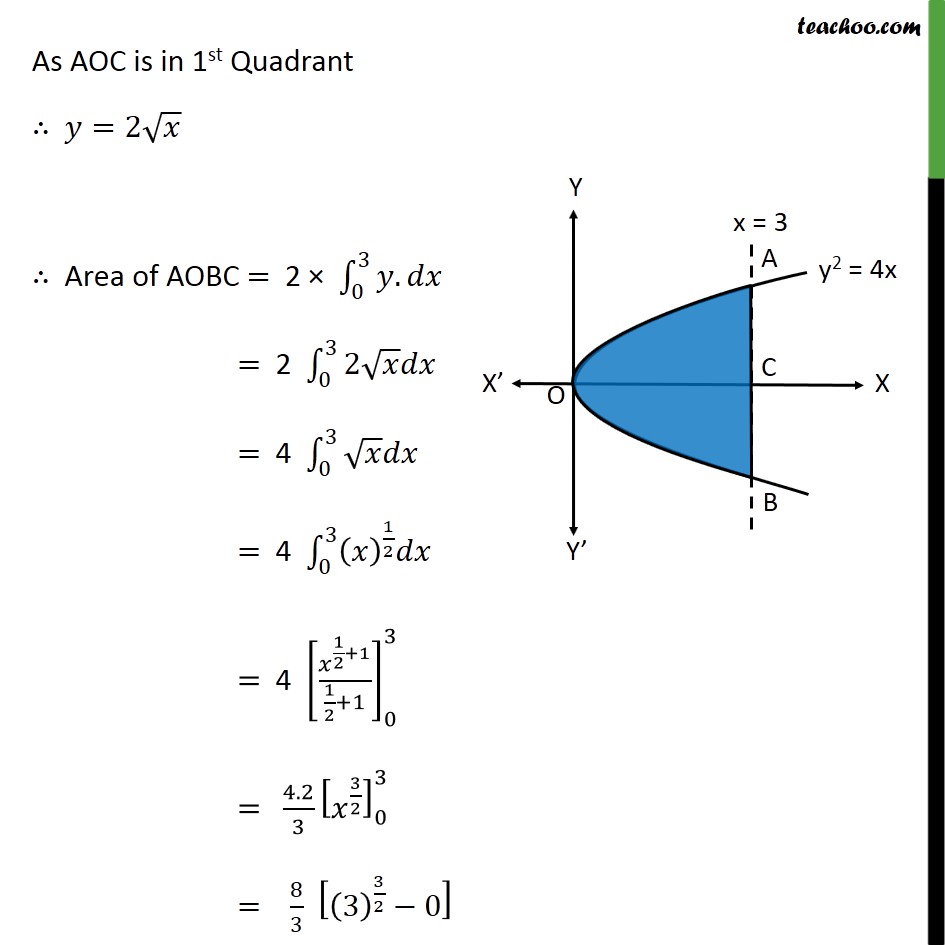



Ex 8 1 11 Find Area Bounded By Y2 4x And Line X 3




Condition On K For X 2 Y 2 12x 6y 4 0 And X 2 Y 2 4x 12y K 0 To Have Simultaneous Solutions X Y Mathematics Stack Exchange




Draw The Graph Of The Linear Equation X 2y 3 And 4x 3y 2 Brainly In




Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube




1 Pt Match The Equations Of The Spheres With One Of Chegg Com



Search Q Y2 Xy 1 X X3 Tbm Isch



How To Draw The Graph Of X 2 Y 2 2x 0 Quora
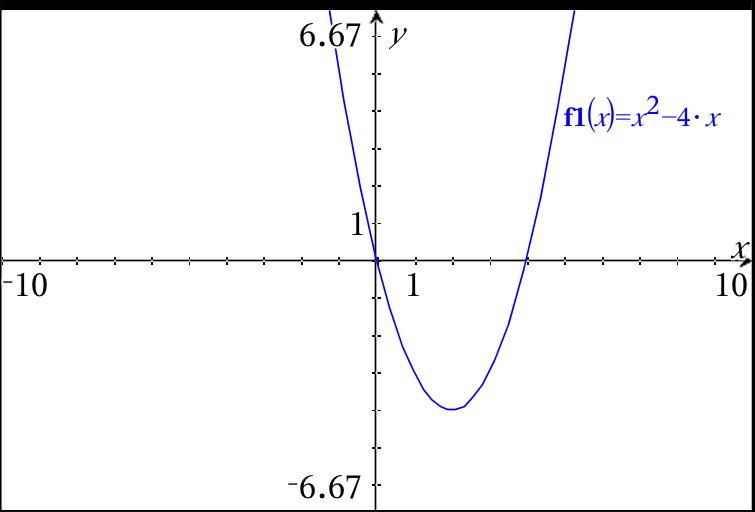



What Is The Graph Of F X X 2 4x Socratic




Use The Functions Y X 2 4x 5 And Y X 1 A Sketch The Graph Of The Two Functions On Same Plane Shade The Region Between The Two




Graph Of Y X 2 4x 5 Novocom Top



Identify The Equation Of The Following Graph Select Chegg Com




Plot A Graph For The Equation Y X 2 4x 1



35 Reduce The Equation X 2 Y 2 Z 2 4x 2y 2z 4 0 To One Of The Standard Forms Classify The Surface And Sketch It Toughstem



Where Do Y X 2 4x 1 And Y 3 X Intersect Mathskey Com
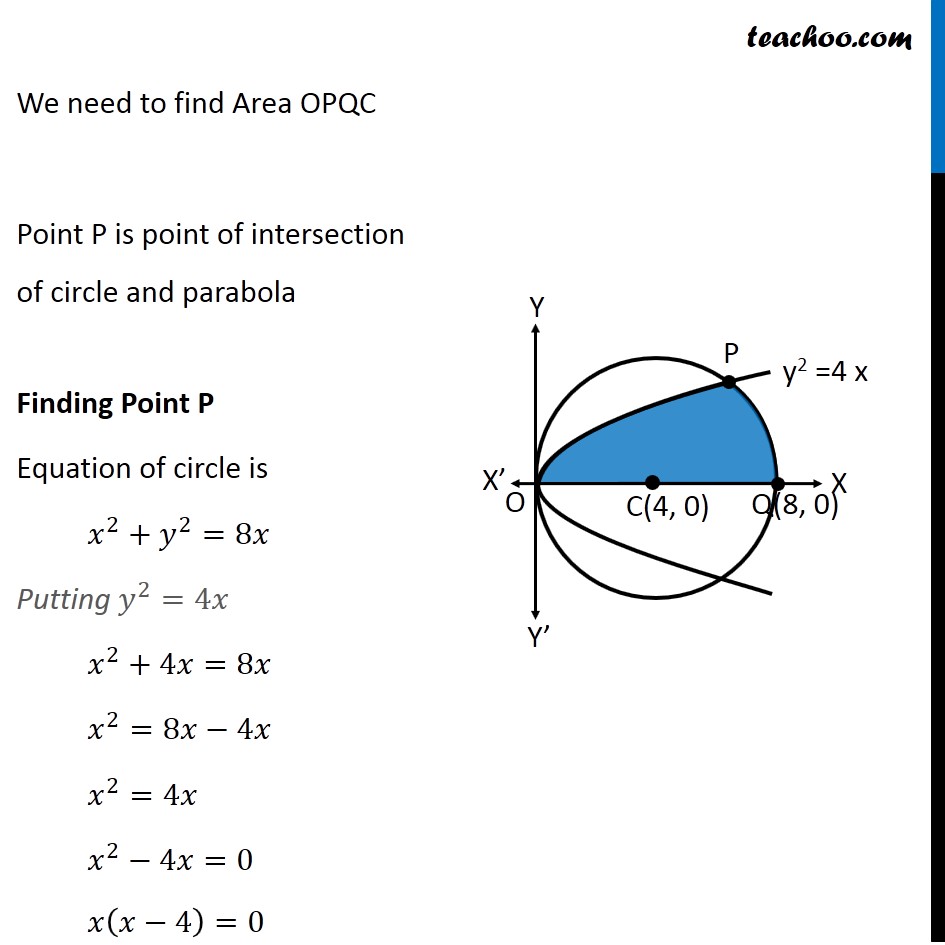



Example 7 Find Area Lying Above X Axis Included B W Circle




Example 14 Prove That Y2 4x X2 4y Divide Area Of Square




Find All Points Of Intersection Of The Graphs Of X 2 4x Y 5 And X Y 9 Study Com




Draw The Graph Of The Follwing Equations 2x Y 2 0 4x 3y 24 0 Y 4 0 Obtain The Vertices Of The Brainly In



Solution At What Points Does The Graph Of Y 2x 2 4x 16 Intersect The X Axis




Graph X 2 Y 2 4 Youtube



Quadratics
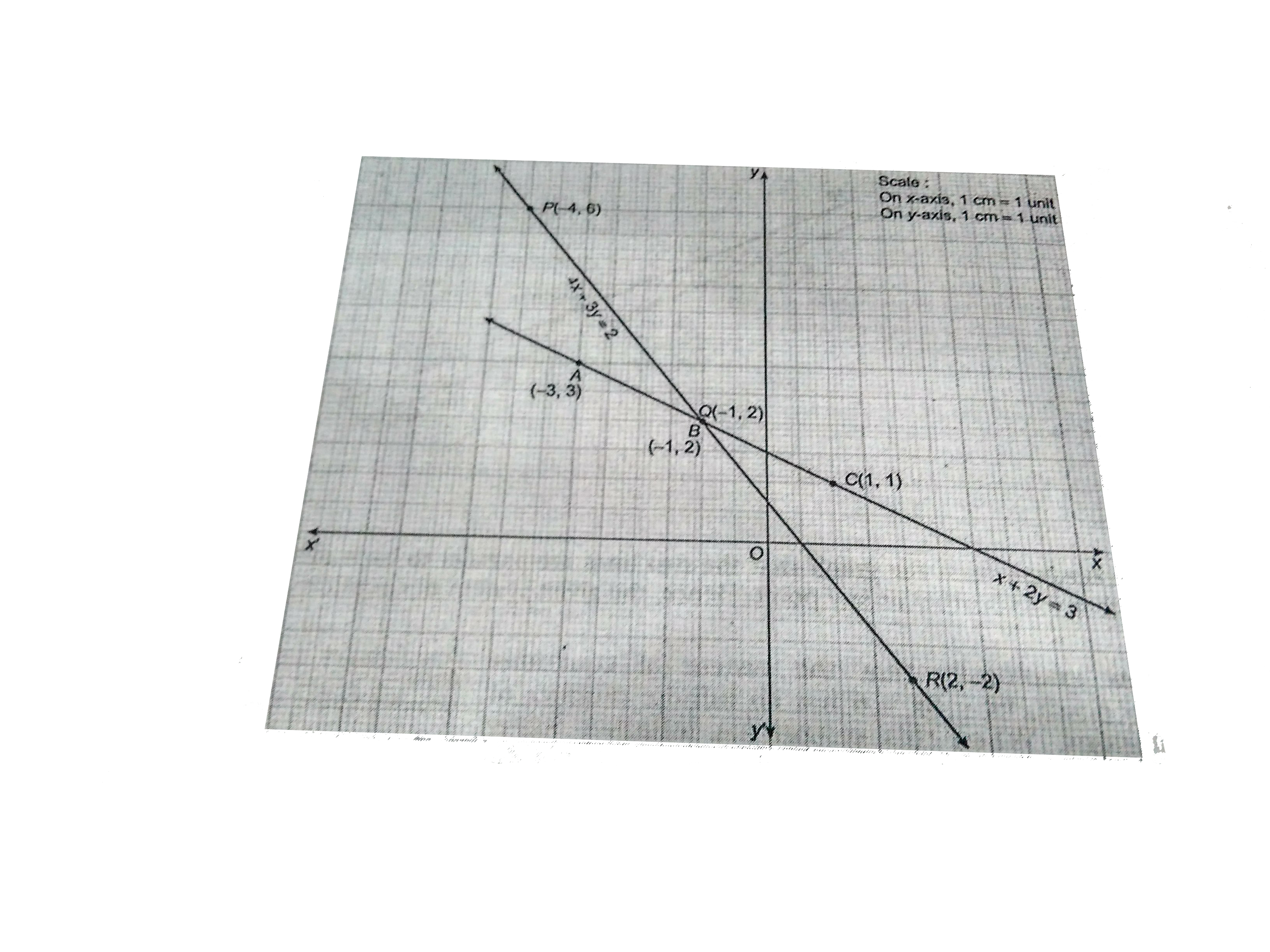



Show Graphically The System Of Linear Equations X 2y 3
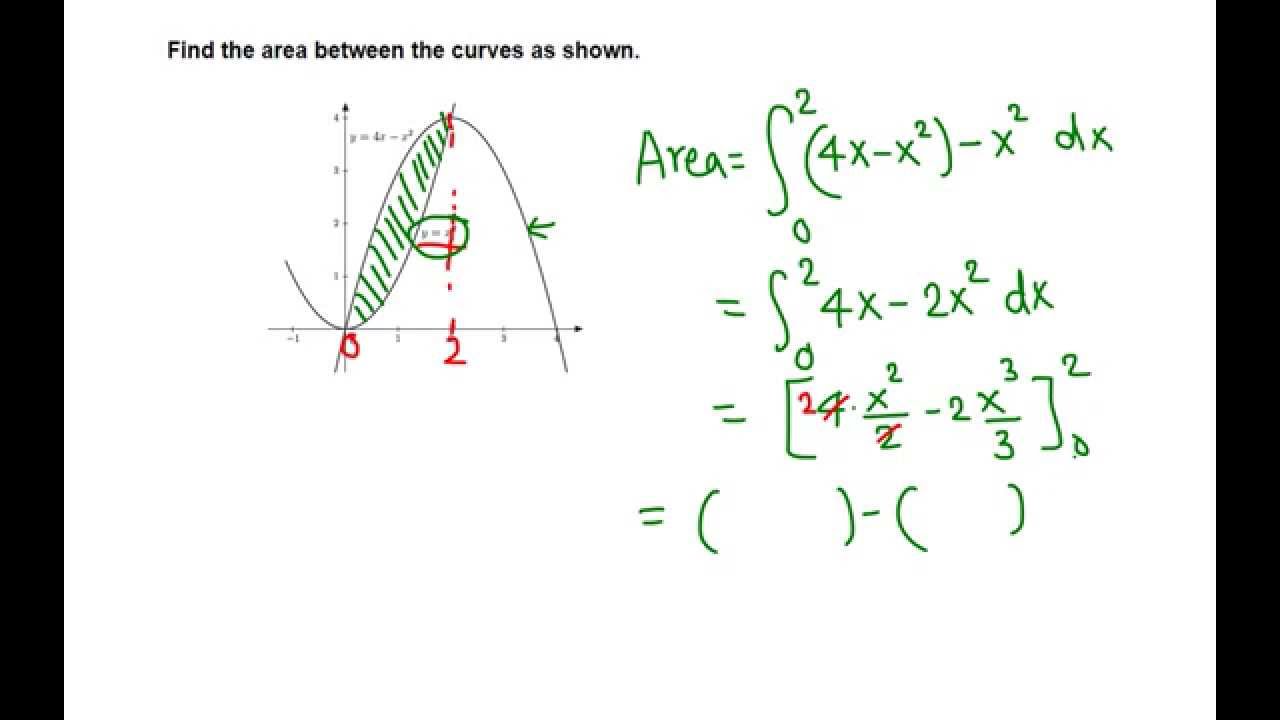



Area Between Y 4x X 2 And Y X 2 Youtube




What Is The Area Of The Region Bounded By The Parabola Y 2 4x And The Line X 1 Quora

