Nov 25, 17 · 展开全部 三角形外角的定理是三角形内角和定理一个推论。 因为三个角的和是180度,而一个内角和它相邻的外角组成了平角,所以这个内角和这个外角的和也是180度,所以这个外角等于不相邻的两个内角之和。 而两个内角必定都大于0度,所以这个外角也一定Oct 22, 17 · 三角形的外角大于与其不相邻的任一内角。 外角定理,在《几何原本》中是第一卷第16命题。三角形の外接円の半径は、内接円の直径以上である ことが分かる。もちろん、正三角形においては、R=2r が成り立つ。 上記では、三角形の外心と内心の距離に注目した公式であったが、外心と傍心の距離 についても同様の公式が成り立つ。
三角形元素外角定理内角三角形png图片素材免费下载 图片编号 Png素材网
三角形の外角の定理
三角形の外角の定理-三角形外角定理的应用 三角形的外角等于与它不相邻的两个内角的和 几何语言: ∵∠acd是 abc的外角 ∴∠acd=∠a∠b 三角形的外角等于与它不相邻的两个内角的和 一个零件的形状三角形外角定理(exterior angle theorem of a triangle)是平面几何的重要定理之一,指三角形的一个外角等于与它不相邻的两个内角的和。 由此可得: 三角形 的 外角 大于任何一个与它不相邻的 内角 。




外角定理と接弦定理などを使うと書いてありますが 解き方がよくわかりません 教えてくだ Clear
三角形内角和定理的证明关注三角形的外角 基础知识精讲 1.三角形按角分类如下 ) 直角三角形(有一个角是直角 三角形 锐角三角形 斜三角形 ) 钝角三角形(有一个角是钝角 2.三角形内角和定理及推论 定理三角形三个内角的和等于180°. 推论1直角三角形的两个锐角互余.Jul 10, 19 · 三角形の角の2等分線と比例 三角形の内角、外角の二等分線での内分点、外分点の関係性 \(\triangle ABCで\angle A\)およびその外角の二等分線が直線AB上に交わる点をM、Nとすると \(ABAC = BMMC=BNNC\) となり、逆も成り立つ。 また上の式が成り立つとき、外角平分线定理定理介绍 编辑 语音 三角形外 角平分线 定理:三角形 外角 的平分线如果和对边的延长线相交,它按照夹相应角的两边的比外分对边。 如下图1,在 中,外角 的平分线 交 的延长线于 ,则
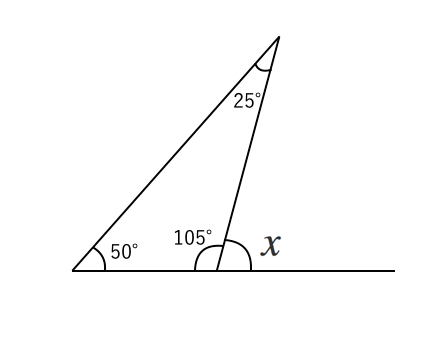
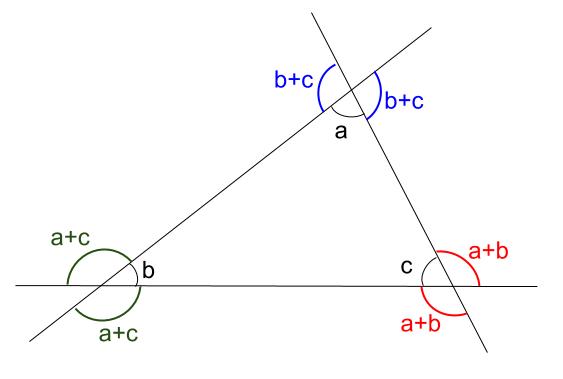
Jun 08, 12 · 三角形の外角を求める外角定理のことを「スリッパの法則」と呼ぶことがあるようです。 外角定理とは「三角形において2つの内角の和は隣り合わない1つの外角と等しい事を示す定理」(Wikipedia外角定理)です。 つまり、下の図で言えば∠Cの外角は∠A∠Bであるということ。三角形の角の二等分線定理(外角) (三角形の角の二等分線に関する公式2) ABCで∠Aの外角の二等分線とBCの延長線との交点をDとするとき、ABAC=BDDC (証明) CからADに平行な直線を引き、ABとの交点をEとする。 ADとECが平行より、∠AEC=∠FAD(同位角)、∠ACE=∠DAC(錯角)。 ∠FAD=∠DACより、∠AEC=∠ACE。 よって、 ACEは二等辺三角形、AE=AC。 ADとECが平行内角と外角 図で隣り合っている赤と青の角の和はそれぞれ180°になっている。 図4 三角形の内角と外角 三角形の内角の和は180°になる >>三角形の内角の和証明 三角形の1つの外角はそれと隣り合わない2つの内角の和に等しい a b x ∠x=∠a∠bである。
Sep 29, · 三角形外角平分线定理是三角形外角的平分线如果和对边的延长线相交,它按照夹相应角的两边的比外分对边。 接下来分享证明方法,供参考。 如图,AD是 ABC中∠BAC的外角∠CAF的平分线。 求证:BA/AC=BD/DC 证明:过C作CE∥DA与BA交于E。 则:BA/AE=BD/DC ∵∠DAF=∠CEA;∠DAC=∠ECA;∠DAF=∠DAC。 ∴∠CEA=∠ECA;∴AE=AC;∴BA/AC=BD/DC。 角円周角 三角形の外角の関係を使う問題 円周角の定理 1つの弧に対する円周角の大きさは一定であり、 その弧に対する中心角の半分である。 三角形の外角は それと隣り合わない2つの内角の和に等しい。重点:三角形的外角及其性质 难点:运用三角形外角性质进行有关计算时能准确地表达推理的过程和方法。 三、教材分析: 教材由学生已经熟悉的三角形的内角和定理引入,然后探索三角形外角的性质。




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




定理 三角形の外角の二等分線と比 定理 Ab Acである Abcの A Okwave
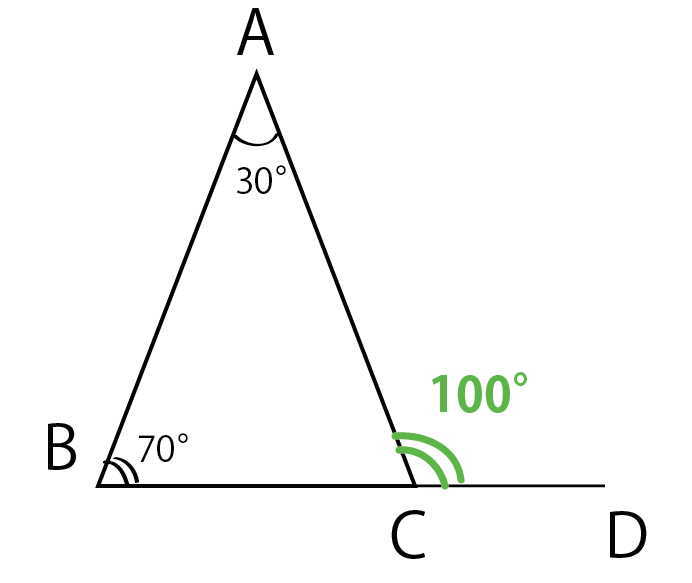
Apr 22, · 三角形外角平分线定理是三角形外角的平分线如果和对边的延长线相交,它按照夹相应角的两边的比外分对边。3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすくSep , 15 · 三角形の外角の定理 って知ってる?? 教科書によると、 三角形の1つの外角は、そのとなりにない2つの内角の和に等しい。 っいう定理があるらしいんだ。 たとえば、 内角60°と30°の三角形があったとしよう。 このとき、 角acd =角bac 角abc = 30° 70° = 100° になるんだ。



図形の調べ方 三角形についてまるわかり 苦手な数学を簡単に



1
三角形の傍心に関する定理 一数学的活動に向けてー 宮城教育大学 萬 仲介 概要: 三角形の傍心(傍接円の中心)に関する二つの定理を紹介す る、これらの証明は「角の二等分線」、l'相似比j、「三角形の面積」等 を用いてなされる。Dec 07, 12 · 2三角不等式 1) 三角形两边之和大于第三边,两边之差的绝对值小于第三边。如果两者相等,则是退化三角形。 2) 三角形任意一个外角大于不相邻的一个内角。 3勾股定理 设直角三角形abc的三顶点a、b、外角 d 等于角 a 加角b 。 外角 d 大于角 a 和角 b 。



外角



三角形元素外角定理内角三角形png图片素材免费下载 图片编号 Png素材网
Sep 09, 19 · また、 CEDにおいて三角形の外角の定理を用いると、 ∠ a = ∠ C E D ∠ C D E ∠ a = ∠ C E D ∠ C D E したがって、 ∠ a = ( 68 ° 32 °) 15 ° = 115 ° ∠ a = ( 68 ° 32 °) 15 ° = 115 ° (解答1終了) 「辺 BC を延長する」 という補助線の引き方でしたね。 「辺 DC を延長する」やり方でもほぼ同様に解けますので、これらは同じ解法として扱います。 また、この解答からわかる三角形的内角和定理:三角形三个内角和等于180°。 推论: (1)直角三角形的两个锐角互余。 (2)三角形的一个外角等于和它不相邻的来两个内角的和。 (3)三角形的一个外角大于任何一个和它不相邻的内角。 注:在同一个三角形中:等角对等边;等边直角三角形の直角の対辺を斜辺という(図 4)。斜辺は、直角三角形の 3 つの辺の中で最も長い。 斜辺を除く残りの 2 辺のことを、直角をはさむ 2 辺と呼ぶ。 直角をはさむ 2 辺 a,b と、斜辺 c の間には、次の関係が成り立つ(ピタゴラスの定理)。 a 2 b 2 = c 2 三角形で、3 辺 a,b,c の長さ




内角と外角の違いがチェバとメネラウスの違いに行き着く件 感じる科学 味わう数学




スリッパの法則 外角定理 スリッパの法則 数学 Tatsuo Yamashita Flickr
多角形の外角の和 内容 n角形の外角の和は、360°である。 証明 三角形の場合 三角形の一つの外角は他の2つの内角に等しいので、外角の和は、内角の和を2回足したことになるので三角形の外角 証明 多角形の場合 一つの頂点の内角と外角の和は180角の2 等分と辺の比に関する定理は、外接円の弧の比まで拡張される。 定理 三角形の1 つの角の二等分線は、 外接円の弧を等しく分ける (bd = cd およびbe = ce) a b c d •• e 定理としては、弧を等分することを言及しただけであるが、実際は次のことも成り立っている。Jun 11, · 三角形的外角性质定理 0611 文/王佳慧 三角形外角定理是平面几何的重要定理之一,定理的内容是三角形的一个外角等于与它不相邻的两个内角的和;三角形的外角大于任何一个与它不相邻的内角。




陳易數學 三角形的外角和 三角形的外角定理 陳易數學 懶人公式包 公式懶人包 Facebook



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
Feb 05, · 三角形の内角・外角 三角形の外角の定理については、意外と忘れられやすいのですが、とてもよく使いますし、便利なものなのでぜひ覚えておき、いつでも使えるようにしましょう。 また、今回のプリントは今後いろいろ応用を利かせることができる問題ばかりです。 しっかり練習してFeb 08, 21 · 三角形内角和定理是:三角形的内角和等于180°。接下来分享三角形内角和定理的证明方法,供参考。三角形内角和定理证明方法证法一:作bc的延长线cd,过点c作ce∥ba,则∠1=∠a,∠2=∠b 资源下载地址 三角形内角和定理是:三角形的内角和等于180°。内角の隣にある外側の角のことを 外角 といいます。 外角の大きさは、 隣にない内角2つの和 に等しくなります。
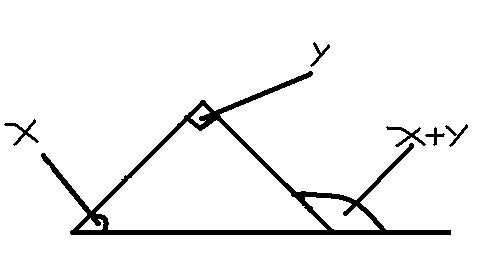



外角の定理 算数勉強会 小学 楽天ブログ




三角形的外角定理 三角形與多邊形的角度 均一教育平台
三角形外角定理(exterior angle theorem of a triangle)是平面几何的重要定理之一,指三角形的一个外角等于与它不相邻的两个内角的和。由此可得:三角形的外角大于任何一个与它不相邻的内角。三角形 四角形 三角形の内角の和 𝟖 ° 平行四辺形 定義2組の対辺がそれぞれ平行な四角形 三角形の外角は、それととなり合わない 2つの内角の和に等しい 2組の 対辺はそれぞれ等しい 三角形の合同条件① 3組の辺がそれぞれ等しい外角定理(がいかくていり)とは、三角形の外角はそれと隣り合わない2つの内角の和に等しいということを示す、ユークリッド幾何学における定理。その形状から、「スリッパの法則」と呼ばれることもある 要出典 。 証明



外角定理 Exterior Angle Theorem Japaneseclass Jp




三角形 角平分线与外角定理专题训练 Word文档在线阅读与下载 无忧文档
三角形と円 三角形と円 円周角と中心角 定理 1つの弧に対する円周角は常に一定で、その弧に対する中心角の に等し い。 点Pを何処にとっても ∠APBの大きさは変わらない。 円周角は常に中心角の半说课人:汤昊 一、教材分析 (一)教材地位 此前学生基本已掌握三角形内角和定理及其证明,在此基础之上推导出本节课的内容,即三角形外角的定义、性质和应用,而三角形外角的性质在今后的推理判断中有着非常重要的作用,因此学好三角形外角的性质和应用可为勾股定理,又稱畢氏定理或毕达哥拉斯定理。设直角三角形的其中一邊 為斜邊,即 的對角 = ,則 = 。



イメージde暗記ポイント 067 外角の定理 中学受験ドクターはプロ講師の個別指導塾 家庭教師



48s96ub7b0z5f Net Gaikaku Senbunhi
三角形の外角の定理 『外角は、その外角のとなり以外の2つの内角の和に等しい』 つまり、下の図の通り。 外角の定理のひみつ外角= + ①三角形の内角の和は180度でした。 だから、三角形的外角(外角定义、定理)(天天练) 学生做题前请先回答以下问题 问题 1:三角形的_____组成的角,叫做三角形的外角. 问题 2:三角形外角定理:三 首页 文档 视频三角形的外角: 三角形的一条边的延长线和另一条相邻的边组成的角,叫做三角形的外角。 ∠1是三角形的外角。 三角形的外角定理: 定理:三角形的一个外角等于不相邻的两个内角和。 定理:三角形的三个内角和为180度。 利用"三角形内角和"性质,可以




3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく



外角




三角形の角度を求める問題 小学生 中学生の勉強
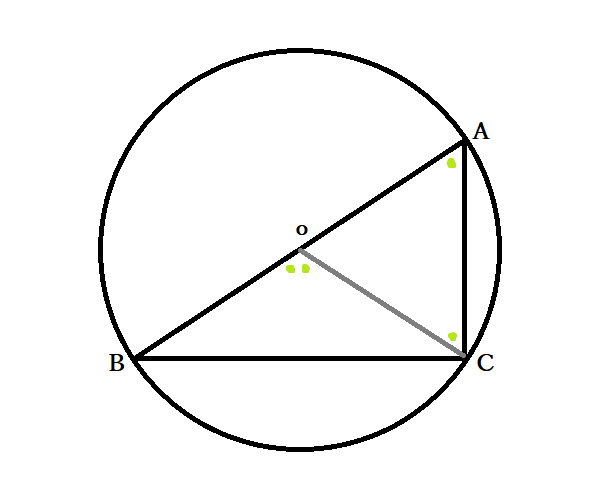



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの幸せblog




円周角 三角形の外角の関係を使う問題
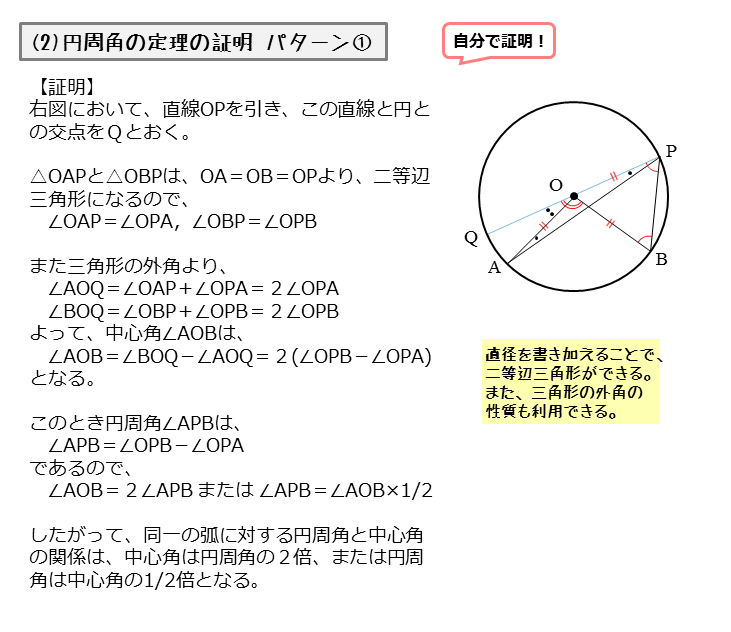



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
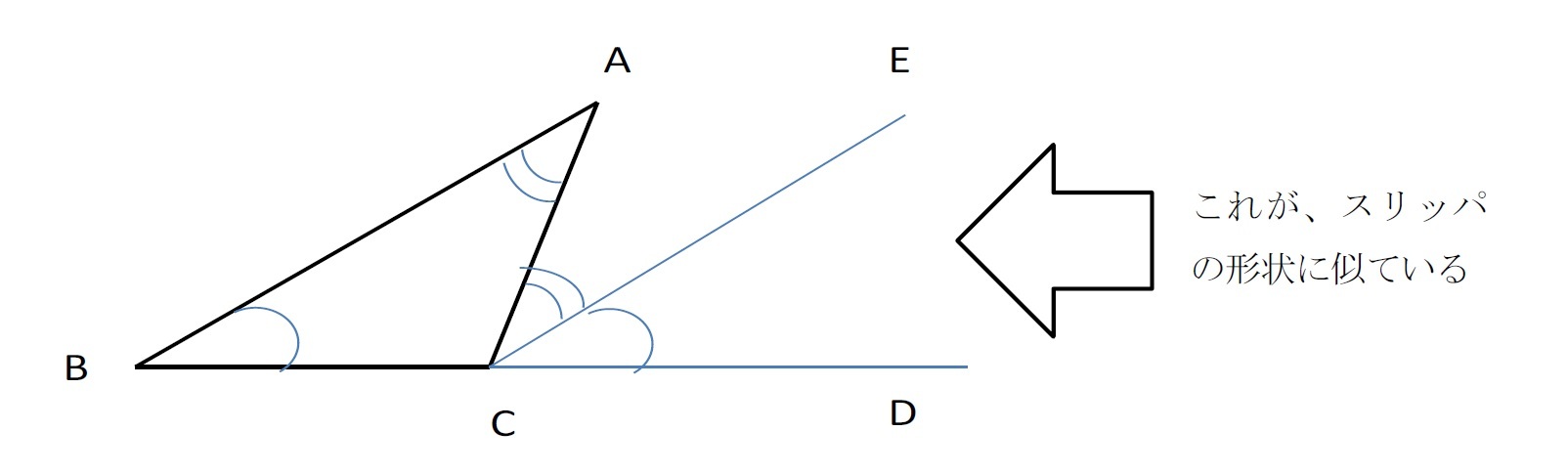



スリッパの法則 って 知っていますか ニッセイ基礎研究所
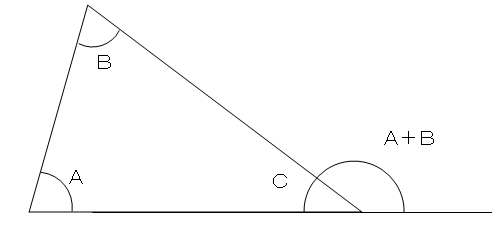



三角形の内角と外角の関係




外角定理と接弦定理などを使うと書いてありますが 解き方がよくわかりません 教えてくだ Clear
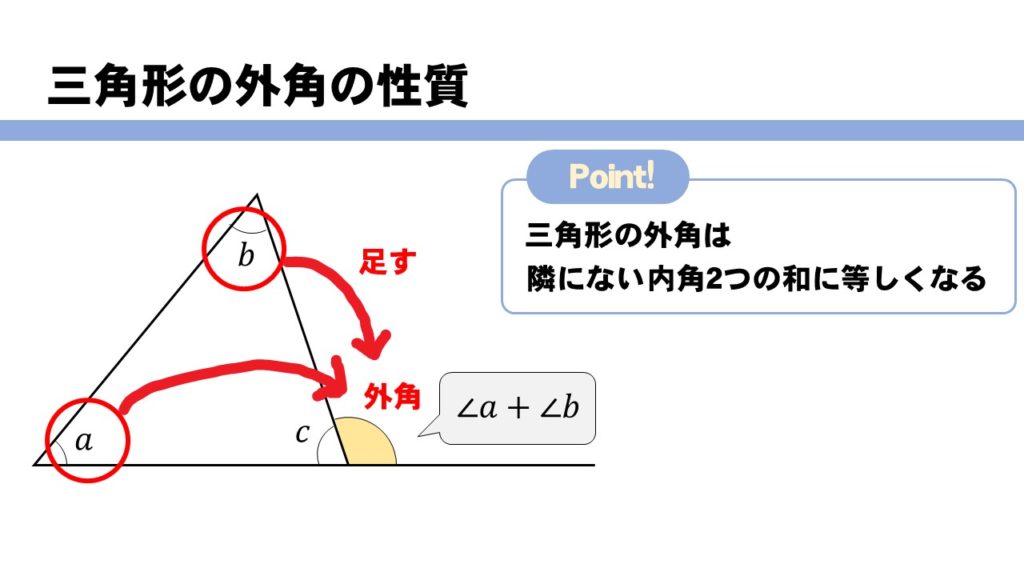



3分なるほど 三角形の内角 外角の性質について解説 数スタ



外角の和の利用



三角形外角角定理 搜索结果 哔哩哔哩 Bilibili




角の2等分線の定理 数学i フリー教材開発コミュニティ Ftext




三角形の内角の和が180 になることの証明 数学fun




算数4年 上 第8回 応用問題解説 最難関問題集 予習シリーズ解説ブログ



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su
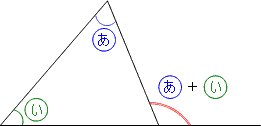



角度の求め方 算数の教え上手 学びの場 Com



図形の扉 三角形の外角の定理




翻轉學習影片 國中 數學 三角形基本性質 三角形外角定理 練習1




三角形の外角と内角の公式 簡単な問題で 外角の求め方を理解しよう 中学や高校の数学の計算問題




図形の外角の定理についてです この問題で白丸をa黒丸をbとして 44 2a 2b Clear
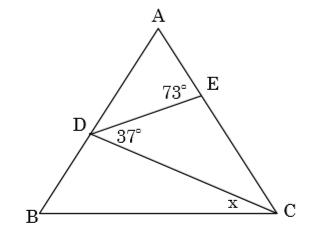



中2数学 三角形の外角の定理の練習問題 Pikuu
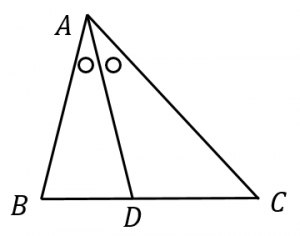



角の二等分線定理 内角 外角それぞれ 具体例で学ぶ数学




第1巻命題16 三角形の外角は内対角より大きい Stoixeia ストイケイア



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




3 三角形外角定理 简书
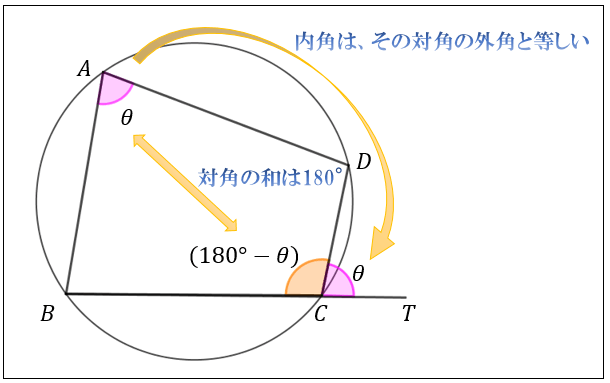



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく



今井塾セミナー
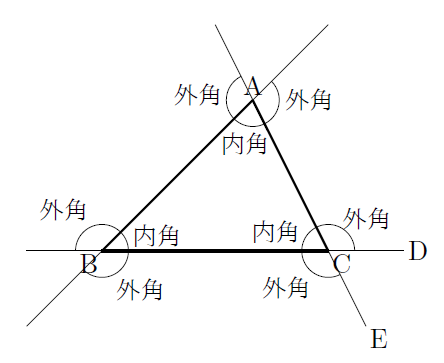



三角形の内角と外角 まなびの学園



Q Tbn And9gcqedkltwbql9i3kzpka2rc4i817awg97onqnm7fs1ljbmrin9gq Usqp Cau



傍接円 傍心について
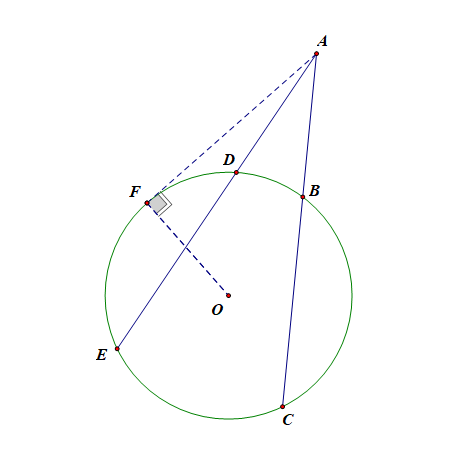



平面几何相关定理 静雅斋数学 博客园




三角形內角和與外角和定理 三角形的性質 均一教育平台




多角形の内角の和 外角の和の公式 数学fun




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット



外角性质定理 腾讯视频



第10回三角形の性質 推理法



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト
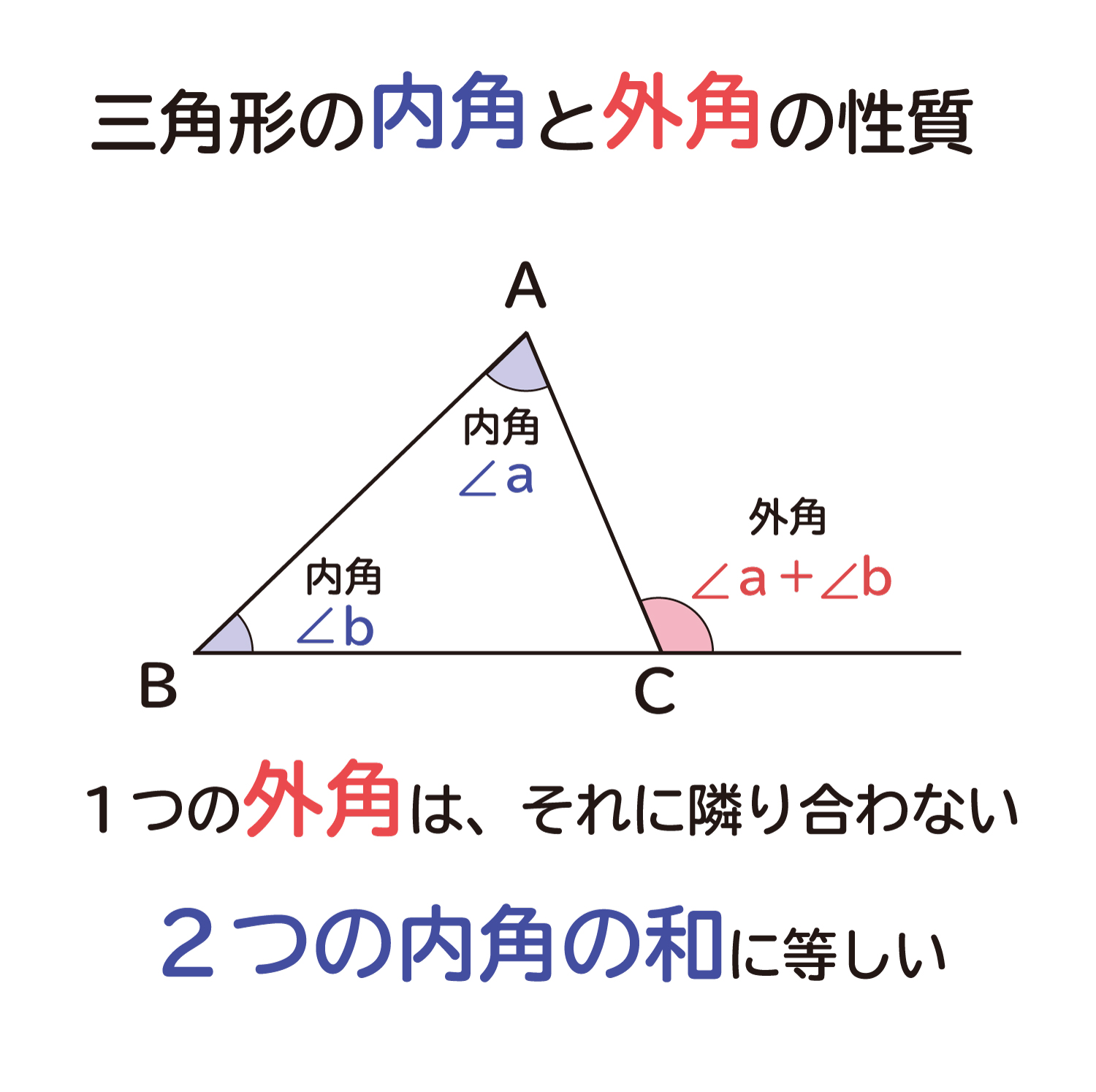



なぜ 三角形の1つの外角は それと隣り合わない2つの内角の和に等しい のか を説明します おかわりドリル




外角定理 Wikipedia




中3数学 円周角の定理を使った定期テスト予想問題 Pikuu



スリッパの法則 って 知っていますか ニッセイ基礎研究所
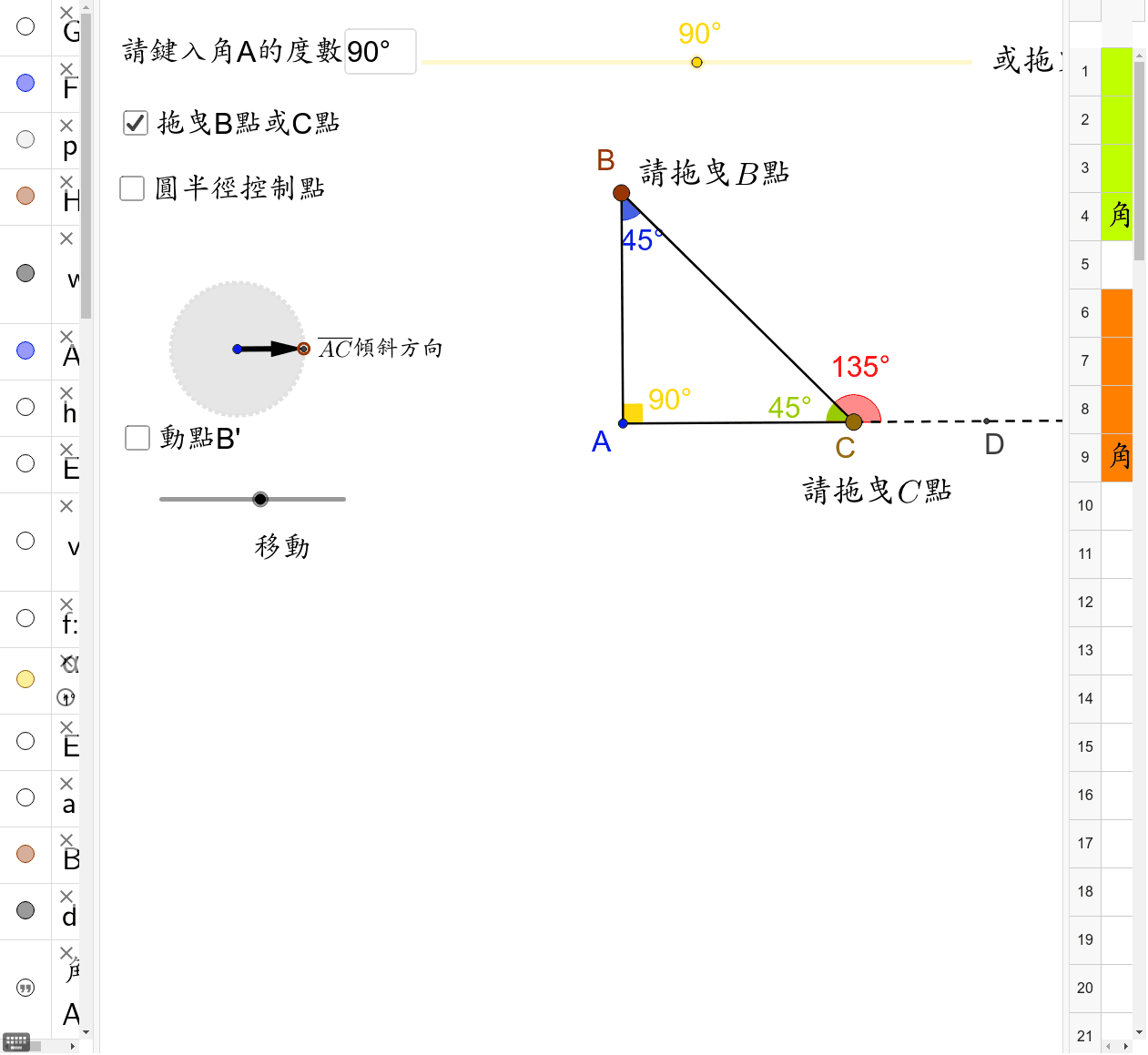



探索三角形外角定理 Geogebra




角の二等分線が図で誰でも一発でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




スリッパの法則 信頼実績 武蔵野進学セミナー 三鷹教室
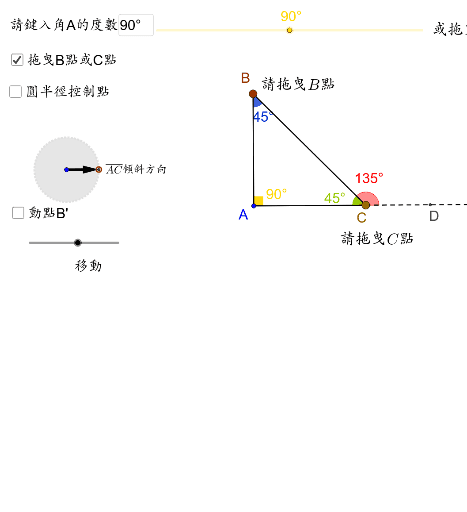



探索三角形外角定理 Geogebra
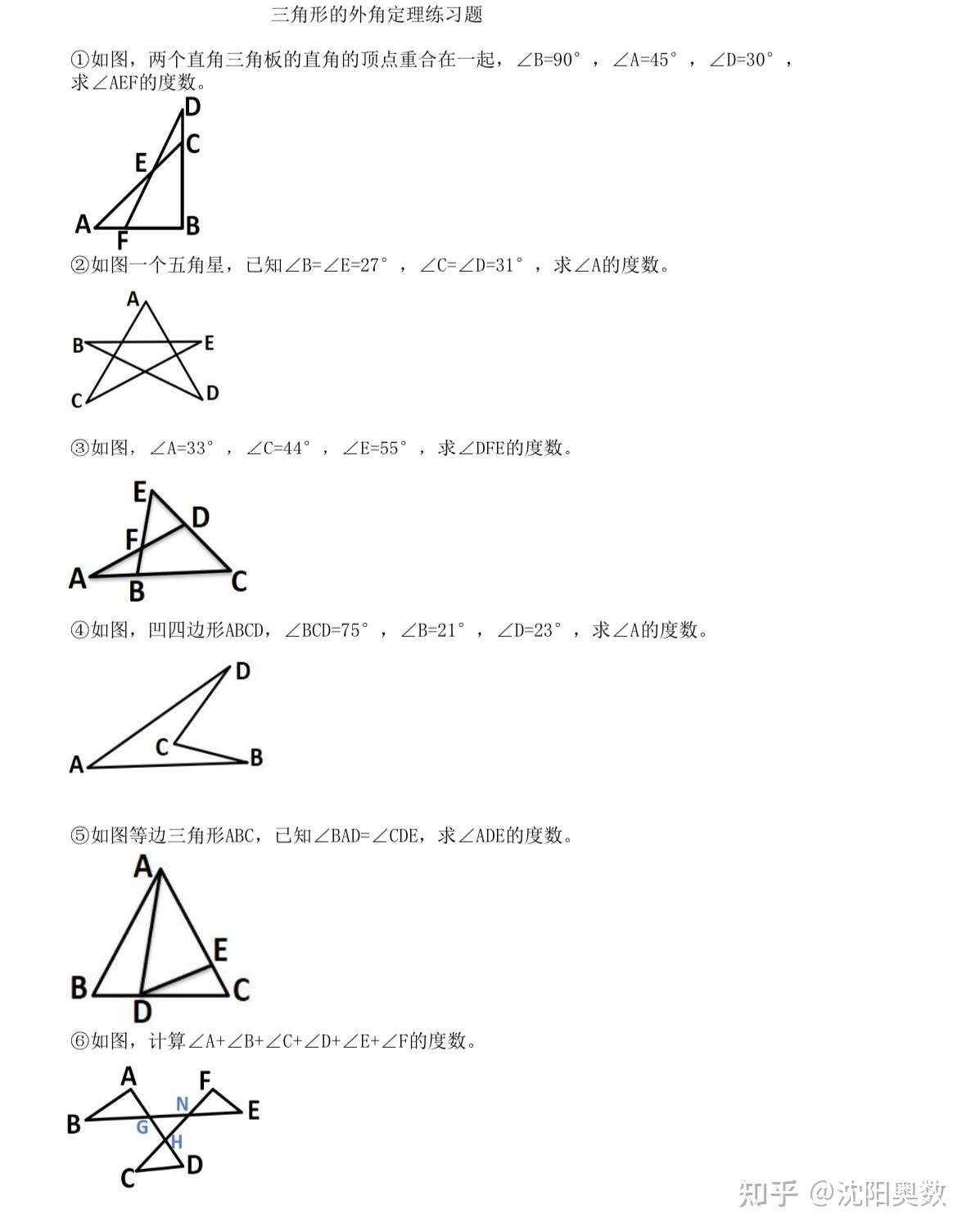



初中几何 三角形外角和定理 自编习题与解析 适合自学 知乎



多角形の内角と外角 思考力を鍛える数学




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学



三角形の角の二等分線定理 外角



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典




中2数学 三角形の内角と外角 例題編 映像授業のtry It トライイット



1




算数図形編 角度 三角形の外角の性質を使いこなそう 中学受験 高校受験パスナビ
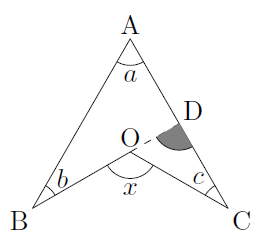



特別な多角形の内角の和 まなびの学園




中学数学 理科 寺子屋塾の復習サイト 三角形関係




数学 中2 48 三角形の内角と外角 基本編 Youtube
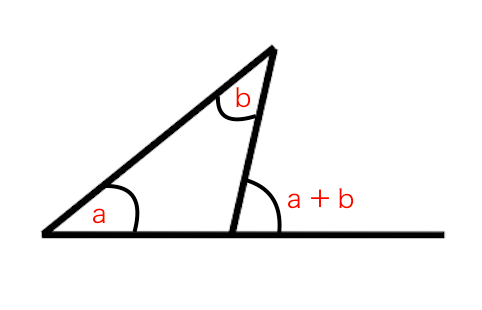



外角の定理とは 苦手な数学を簡単に



3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく




3 三角形外角定理 简书




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora




三角形の外角の性質 Youtube
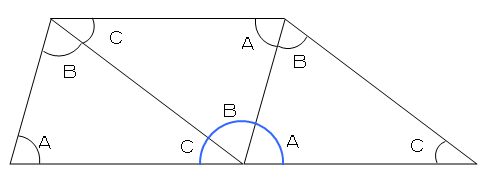



三角形の内角と外角の関係



三角形外角定理 腾讯视频
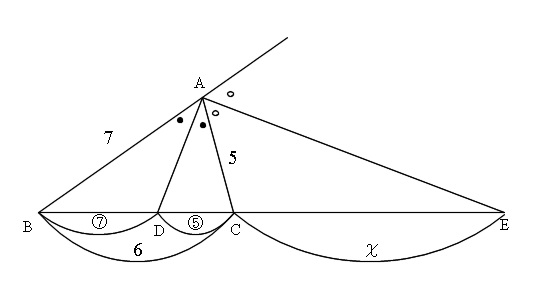



内角の二等分線と外角の二等分線の定理の覚え方と使い方




外角の難問 市ヶ谷 中学受験credoのブログ




中2数学 複雑な多角形 角の和 応用問題
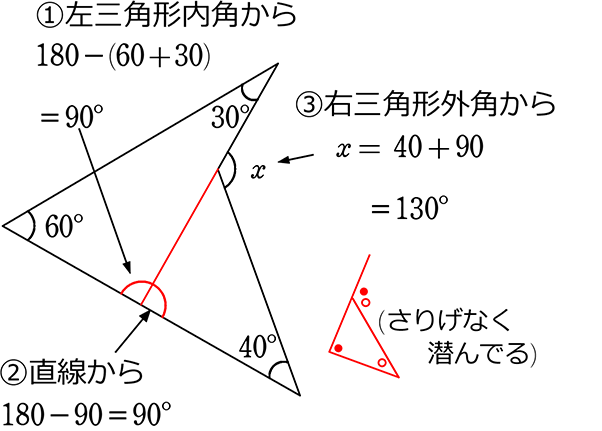



中学数学 平面図形と平行線の性質



三角形の角の二等分線定理
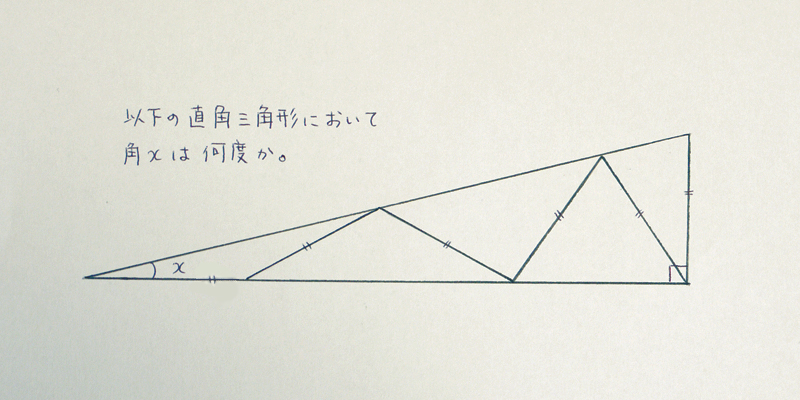



ナー 娘が外角定理を習ったので 有名な美しい問題を出してみたら んーーー 見た感じ15度に見える と まさかのアプローチで正答を出されて参りました



図形の問題を得意にしたい




Sc24 同じことの繰り返しを簡単に表現する Scratch99 ページ




三角形外角定理 搜狗百科



凹んだ四角形の内角と外角の関係 中2 tさんからの質問に答えますv O A Day In Our Life




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学
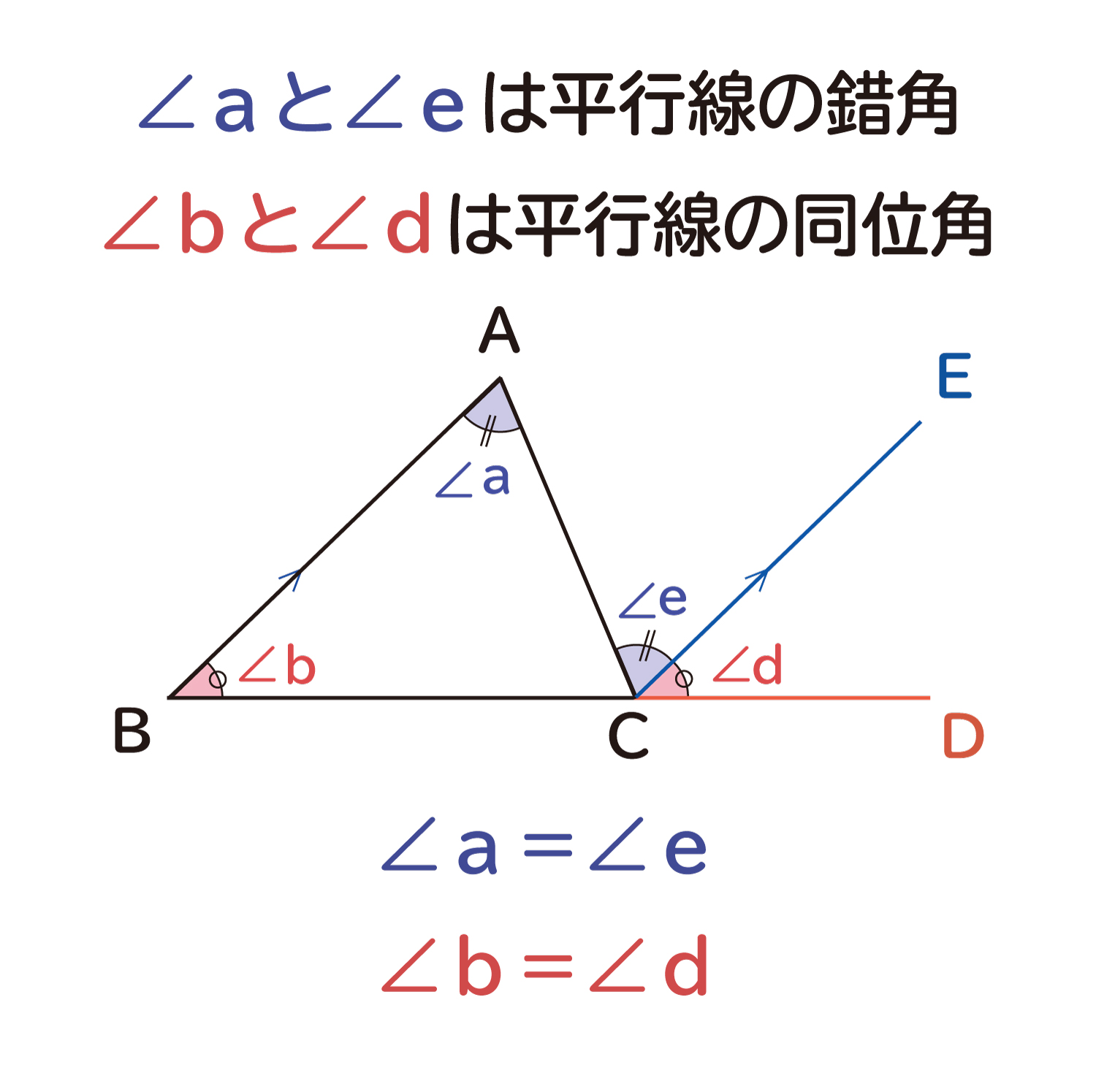



なぜ 三角形の1つの外角は それと隣り合わない2つの内角の和に等しい のか を説明します おかわりドリル




三角形外角定理 Youtube




陳易數學 三角形的外角和 三角形的外角定理 陳易數學 懶人公式包 公式懶人包 Facebook




三角形內角定理與外角定理應用 Youtube
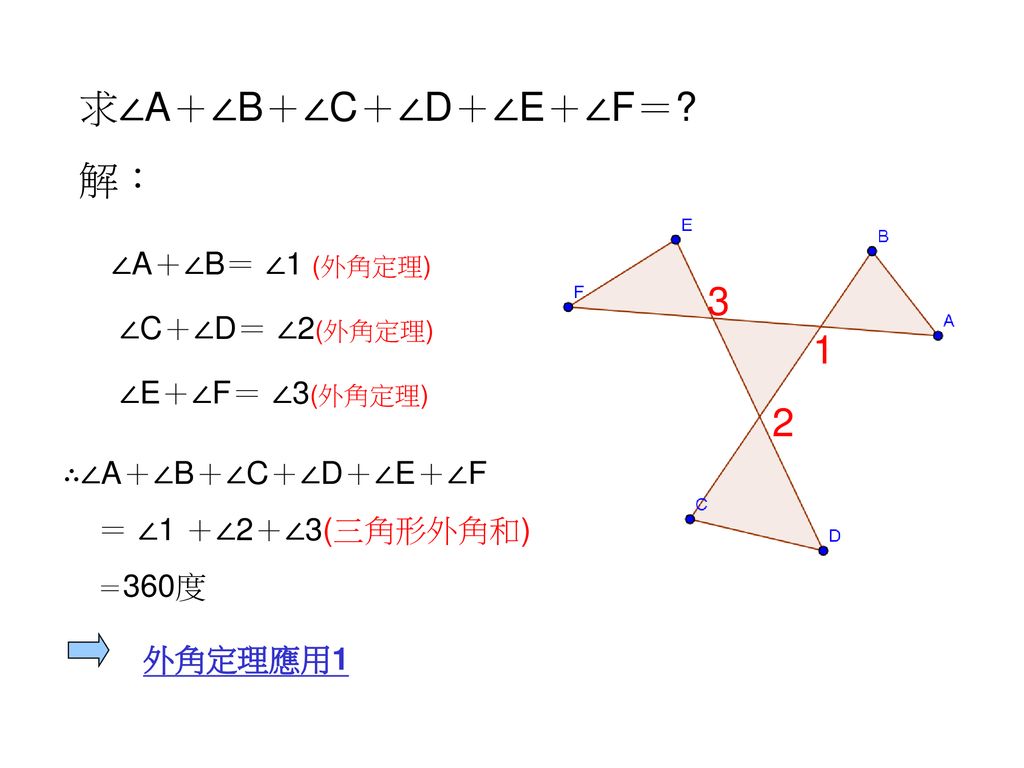



多邊形的內角與外角 Ppt Download



Search Q E4 Ba 8c E7 Ad E8 Be Ba E4 B8 E8 92 E5 Tbm Isch



高校入試数学 円と三平方の定理の利用の融合問題
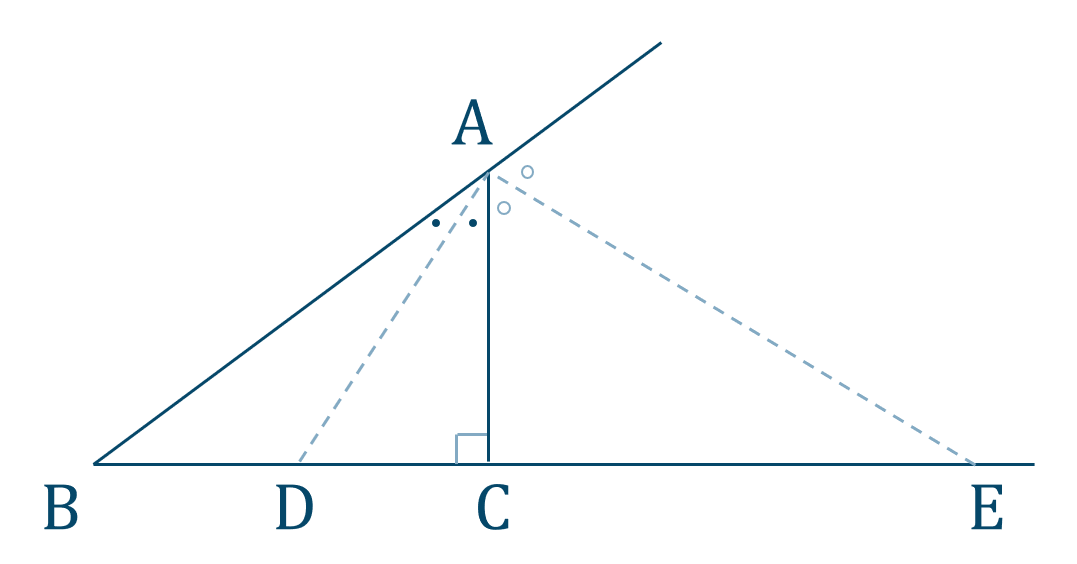



数学a 角の二等分線と比の使い方とコツ 教科書より詳しい高校数学




1 Adza 1 2 Descubre Como Resolverlo En Qanda




三角形的內角與外角 張貼者 May 4 15 10 34 Pm魏恩立 三角形的內角與外角 一 內角 外角 三角形abc 中 角 A 角 B 角 C 稱為 三角形abc 的三內角 而與內角互補的鄰角稱為外角 1 外角和任一三角形的三外角和皆為360 如右圖 角 1 角 2

